Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 119

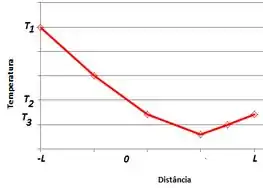
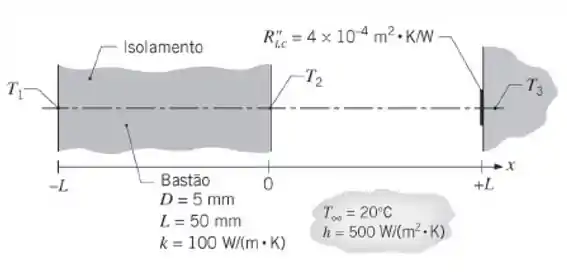
Considere um bastão de diâmetro D, condutividade térmica k e comprimento 2L que é perfeitamente isolado em uma parte do seu comprimento, – L   ≤   x   ≤   0 , e na outra parte, 0   ≤   x   ≤   + L , troca calor por convecção com um fluido ( T ∞ , h). Uma extremidade é mantida a T 1 , enquanto a outra é separada de um sumidouro de calor a T 3 por uma resistência térmica de contato interfacial, R ' ' t , c .

  1. Esboce a distribuição de temperaturas em coordenadas T – x e identifique suas principais características. Suponha que T 1 > T 3   > T ∞ .
  2. Deduza uma expressão para a temperatura no ponto central T 2 em termos dos parâmetros térmicos e geométricos do sistema.
  3. Para T 1 = 200 ° C , T 3 = 100 ° C e as condições fornecidas no esquema, calcule T 2 e represente graficamente a distribuição de temperaturas. Descreva as características principais da distribuição e a compare com o seu esboço feito na parte (a).

Passo 1

Respirem fundo galerinhaa !!

Vamos pra mais umaa ...

Na letra (a) nós queremos esboçar para a distribuição de temperatura, não é?

Na parte isolada do bastão o sistema vai apresentar condução unidimensional e, por isso, a temperatura tenderá a cair linearmente de T 1 até T 2 , então distribuição linear !!

Quando não há isolamento a superfície se comporta como uma superfície estendida unidimensional e, por isso, a queda de temperatura se comporta de maneira não linear de T 2 até T 3 .

Esboçando esta situação:

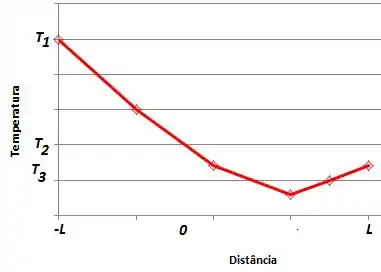
A letra (a) tá prontíssimaa, bora pra (b) ?!

Passo 2

Booom, a letra (b) nos pede pra achar uma função para T 2 , certo?

Das nossas questões anteriores nós obtivemos que:

θ ( x ) = C 1 e m x + C 2 e - m x + M m 2

Onde:

m = 4 h k D

M = q ˙ k

Como não temos calor sendo adicionado ao sistema:

θ x = C 1 e m x + C 2 e - m x

Para T 2 nós temos o ponto x = 0 :

θ 0 = C 1 e 0 + C 2 e 0

θ 0 = C 1 + C 2

Se:

θ = T - T ∞

Então:

T 2 = T ∞ + C 1 + C 2

É isso aí, acabamos a letra (b) e vamos seguindo !!

Passo 3

Na letra (c) nós queremos achar T 2 , sabendo que:

T 1 = 200 ° C + 273 = 473   K

T 3 = 100 ° C + 273 = 373   K

Podemos começar representando a Lei de Fourier de condução para o ponto x = 0 :

q x 0 = - k A c d θ d x

Como d θ d x é a variação de θ com relação a x, podemos usar o ponto x = 0 e x = - L :

- k A c d θ d x = - k A c θ 0 - θ 1 0 - - L

- k A c d θ d x = - k A c θ 0 - θ 1 L

d θ d x = θ 0 - θ 1 L

Substituindo θ :

d d x C 1 e m x + C 2 e - m x = θ 0 - θ 1 L

E derivando:

C 1 m e m x - C 2 m e - m x = θ 0 - θ 1 L

Como temos x = 0 :

C 1 m - C 2 m = θ 0 - θ 1 L

m ( C 1 - C 2 ) = θ 0 - θ 1 L

m L ( C 1 - C 2 ) = C 1 + C 2 - θ 1

Substituindo θ 0   e   θ 1 :

m L C 1 - C 2 = C 1 + C 2 - T 1 + T ∞

Vamos precisar por a mão na massa agora e ver nossos dados:

h = 500 W m 2 K

D = 5   m m = 0,005 m

k = 100 W m K

L = 50   m m = 0,05   m

T ∞ = 20 ° C + 273 = 293   K

Achando m:

m = 4 500 W m 2 K 100 W m K 0,005 m = 63,25   m - 1

Na fórmula:

63,25   m - 1 0,05   m ( C 1 - C 2 ) = C 1 + C 2 - 180   K

3,162 C 1 - 3,162 C 2 = C 1 + C 2 - 180   K

- 2,162 C 1 + 4,162 C 2 = 180   K

C 1 = 4,162 C 2 - 180 2,162

Vamos guardar esta informação, ok?

Passo 4

Agora vamos representando a Lei de Fourier de condução para o ponto x = L :

q x L = - k A c d θ d x

No ponto 3 nós podemos reescrever q x em função da resistência térmica:

- k A c d θ d x = θ ( L ) - θ 3 R ' ' t , c A c

Substituindo θ :

- k A c d d x C 1 e m x + C 2 e - m x = A c C 1 e m L + C 2 e - m L - θ 3 R ' ' t , c

E derivando:

- k ( C 1 m e m L - C 2 m e - m L ) = C 1 e m L + C 2 e - m L - θ 3 R ' ' t , c

Substituindo θ 3 :

- k ( C 1 m e m L - C 2 m e - m L ) = C 1 e m L + C 2 e - m L - T 3 + T ∞ R ' ' t , c

Substituindo nossos valores:

- 100 W m K 4,162 C 2 - 180 2,162 63,25   m - 1 e 63,25   m - 1 0,05   m - C 2 63,25   m - 1 e - 63,25   m - 1 0,05   m = 4,162 C 2 - 180 2,162 e 63,25   m - 1 0,05   m + C 2 e - 63,25   m - 1 0,05   m - 373   K + 293   K 4 × 10 - 4 m 2 K W

C 2 = 43,764

Achando C 1 :

C 1 = 0,99

E agora é só achar T 2 usando a fórmula da letra (b):

T 2 = 293 + 0,99 + 43,764

T 2 = 337,3   K

Em graus Celsius:

T 2 = 64,75 ° C

Quando plotamos o gráfico:

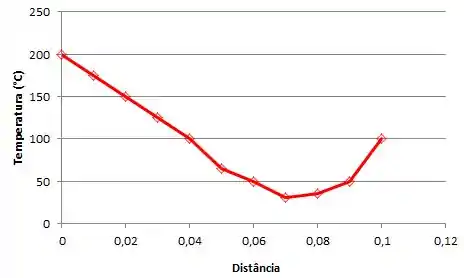
De acordo com o que propomos na letra (a), certinho?

Legal, não foi?

Resposta

  2. T 2 = T ∞ + C 1 + C 2 ;
  3. T 2 = 64,75 ° C .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma casca esférica, com raios interno e externo r i e r e , respectivamente, está cheia de um material gerador de calor que fornece uma taxa volumétrica de geração ( W / m 3 ) e uniforme igual a q ˙ .
Um vaso esférico, usado como reator para produzir fármacos, tem uma parede de aço inoxidável ( k = 17W / m K ) com 10m m de espessura e diâmetro interno de 1m . A superfície externa do vaso é exposta
Uma esfera oca de alumínio, com um aquecedor elétrico no centro, é usada em testes para determinar a condutividade térmica de materiais isolantes. Os raios interno e externo da esfera são 0,15 e 0,18m
Uma tubulação de vapor com 0,12 m de diâmetro externo está isolada termicamente por uma camada de silicato de cálcio. (a) Se o isolante possui uma espessura de 20 mm e as suas superfícies interna e ex
Um aquecedor elétrico delgado é enrolado ao redor da superfície externa de um longo tubo cilíndrico cuja superfície interna é mantida a uma temperatura de 5°C. A parede do tubo possui raios interno e