Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 121
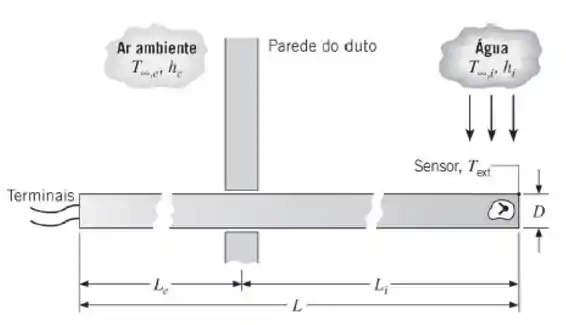
Um sensor com comprimento total L = 200 mm e diâmetro D = 12,5 mm está inserido através da parede de um duto de tal forma que uma fração do seu comprimento, identificada pelo comprimento de imersão Li, fica em contato com a corrente de água, cuja temperatura, , deve ser determinada. Os coeficientes convectivos na fração imersa e na fração exposta ao ar
ambiente são e , respectivamente. O sensor possui uma condutividade térmica de e o seu contato térmico com a parede do duto é ruim.
- Deduza uma expressão para avaliar o erro da medida, , que é a diferença entre a temperatura da extremidade do sensor, , e a temperatura da água, . Sugestão: Defina um sistema de coordenadas com a origem na parede do duto e trate o sensor como duas aletas que se estendem para dentro e para fora do duto, mas que possuem a mesma temperatura na base. Use os resultados para o Caso A na Tabela 3.4.
- Com as temperaturas da água e do ambiente a 80 e 20°C, respectivamente, calcule o erro da medida, , em função do comprimento de imersão do sensor para as condições Li/L = 0,225; 0,425 e 0,625.
- Calcule e represente graficamente os efeitos da condutividade térmica do sensor e da fator convectivo da água (hi) no erro de medida.
Passo 1
Boom galerinhaa, vamos seguir??
Como a temperatura vai aumentando do ar ambiente até alcançar a temperatura da água nós teremos uma distribuição não linear, partindo de , ponto inicial, até , ponto final.
Nós vamos assumimos aqui dois valores de x, o que vai do ponto inicial até , onde está a parede, ok? Se reescrevermos isso , mesma coisa certo?
Agora o está localizada da parede até a água quente, ou melhor, .
Na letra (a) nós precisamos achar só que para isso nos foi sugerido usar o Caso A da Tabela 3.4:
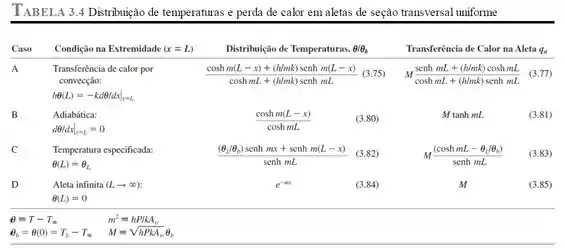
Então nós teremos:
Se olharmos esta fórmula na região i, com a temperatura indo :
Quando nós teremos que :
Sendo assim:
Podemos chamar:
E chegamos ao fim da letra (a) !!
Passo 2
Sabendo que:
Nós queremos calcular aqui e o erro associado a , ok?
Para calcular nós precisamos lembrar que a taxa de transferência de calor através da aleta é igual para as duas partes, como a temperatura da parte i é maior o fluxo de calor está deixando ela e indo em direção à parte o:
Usando ainda o Caso A da Tabela para transferência de calor nas aletas:
Chamando:
Então:
Substituindo M pelo que a tabela nos disse:
Substituindo e :
Agora vamos prestar atenção aqui !!
Diferentes razões nos dão diferente Com isso obtemos diferentes e .
Agora nós vamos usar nossos dados e colocar em forma de tabela:
Então, a sonda é mais precisa quando mais de seu comprimento é exposto à água, ou seja, maior
Agora que já achamos a letra (b) vamos seguindo, certo?
Passo 3
Na letra (c) nós precisamos calcular e representar graficamente os efeitos da condutividade térmica do sensor e do fator convectivo da água (hi) no erro de medida.
Quando alteramos estes dois fatores nós vamos mudar também os valores de A, B e C. Então nós vamos calcular o erro usando a fórmula que vimos anteriormente e comparar graficamente usando três casos:
No gráfico:
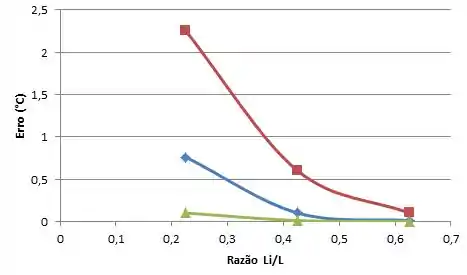
Portanto, quanto menor a condutividade térmica e o fator convectivo, menor será o erro! Ao contrário, quando diminuímos o fator convectivo nós aumentamos o erro !!
O que acharam desta?
