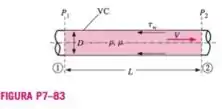
A queda de pressão através de uma secção longa de um tubo redondo pode ser escrita em termos da tensão de cisalhamento ao longo da parede. A tensao de cisalhamento que age na parede do fluido é mostrada na Figura . A região sombreada é um volume de controle composto pelo fluido do tubo entre as posições axiais e . Existem dois parâmetros adimensionais relacionados a queda de pressão: o número de Euler Eu e o fator de atrito de Darcy .
(a) Usando o volume de controle representado na Figura , gere uma relacão para em termos de Eu (e de quaisquer outras propriedades ou parâmetros do problema que sejam necessários).
(b) Usando os dados e as condições experimentais do Problems (Tabela ), trace o fator de atrito de Darcy como função de Re. O mostra independência do número de Reynolds para valores grandes de Re? Neste caso, qual é o valor de para um Re muito alto?
Passo 1
Bom gente, para resolvermos essa questão, devemos avaliar as nossas condições. Em questões de pressão e tensão de cisalhamento em tubos, quando o perfil é completamente desenvolvido isso nos garante que em qualquer ponto a velocidade é a mesma.
Essas forças viscosas e de pressão se contrabalançam, daí o momento se conserva:
Cada uma dessas expressões é escrita da seguinte forma:
A tensão com sinal negativo pois é uma força que aponta para a esquerda. Assim, igualando as tuas expressões, temos:
Agora, relacionando com o número de Euler (), como , temos:
E, por fim, atribuindo o fator de atrito de Darcy , podemos reescrever a equação acima da seguinte forma:
Passo 2
Para o item (b), vamos usar a seguinte tabela do problema :
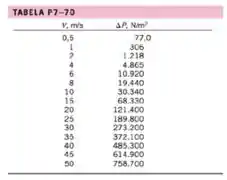
Com , , e . Usamos os dados no Excel para facilitar a nossa vida e facilitar os cálculos. Assim, temos:
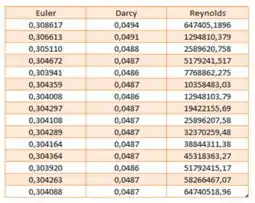
E plotamos o seguinte gráfico:
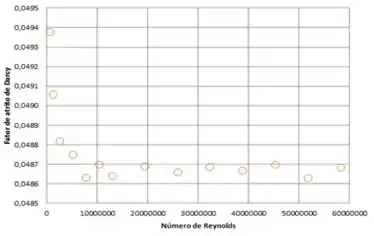
A partir desse gráfico, podemos perceber que o valor de mostra independência para valores de Reynolds maiores de , ou seja, o fator de atrito tende a se estabilizar. Da mesma forma, acontece com o numero de Euler.
E, por fim, pelo gráfico, o valor extrapolado de em função de é de cerca de . Comprovando:
Prontinho!!
Resposta
(a)
(b) Sim, .