Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 4.Problemas - Ex. 49

Um canal por onde passam gases quentes de exaustão apresenta uma seção transversal quadrada de 4 00   m m de lado. As paredes são construídas com tijolos refratários com 20 0   m m de espessura e condutividade térmica de 1,5 5   W / m · K . Calcule a perda de calor dos gases, por unidade de comprimento, quando as superfícies interior e exterior do canal são mantidas a 350 e 25 ° C , respectivamente. Use uma malha com espaçamento de 100   m m .

Passo 1

E aí, bora resolver essa questão comigo?

Se ajeita aí e vamos lá!

Começamos o nosso problema dividindo o duto trabalhado em 4 partes:

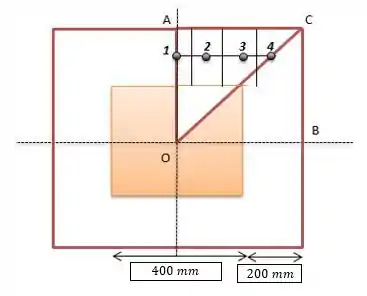
Podemos perceber que o duto simétrico em relação ao eixo A O , O B e O C .

Desse modo, podemos observar que uma seção O A C e O B C são simétricas e adiabáticas e representam uma parte de oito.

Como estamos analisando os pontos internos só teremos condução aqui.

Possuindo simetria e percebendo que temos nós internos, as especificações serão dadas por:

T i = 1 4 ∑ T v i z

Então:

T 1 = 1 4 T e x t + T i n t + 2 T 2 = 0,25 ⋅ 350 + 25 + 2 T 2

T 2 = 1 4 T 1 + T i n t + T 3 + T e x t = 0,25 ⋅ 350 + 25 + T 1 + T 2

T 3 = 1 4 T 2 + T i n t + T 4 + T e x t = 0,25 ⋅ 350 + 25 + T 4 + T 2

T 4 = 1 4 T i n t + 2 T 3 + T i n t = 0,25 ⋅ 25 + 2 T 3 + 25

Com auxílio de programas matemáticos, obtemos:

T 1 = 184 ° C

T 2 = 180,3 ° C

T 3 = 162,2 ° C

T 4 = 93,6 ° C

Passo 2

Agora que possuímos as temperaturas dos pontos, percebemos que cada ponto vai perder calor por convecção para o ambiente, então:

q ˙ = q 1 + q 2 + q 3 + q 4

Abrindo:

q ˙ = k ∆ x 2 T 1 - T e x t ∆ y + k ∆ x T 2 - T e x t ∆ y + k ∆ x T 3 - T e n t ∆ y + k ∆ x T 4 - T e x t ∆ y

q ˙ = k ∆ x ∆ y 1 2 T 1 - T e x t + T 2 - T e x t + T 3 - T e n t + T 4 - T e x t

Como ∆ x = ∆ y :

q ˙ = k 1 2 T 1 - T e x t + T 2 - T e x t + T 3 - T e n t + T 4 - T e x t

Substituindo os dados:

q ˙ = 1,55 ⋅ 1 2 184 - 25 + 180,3 - 25 + 162,2 - 25 + 93,6 - 25

q ˙ = 683   W / m

Como temos todas as partes:

q ˙ t o t a l = 8 ⋅ 683

q ˙ t o t a l = 5464   W / m

E assim a gente finaliza a nossa questão!

Até a próxima!

Resposta

q ˙ t o t a l = 5464   W / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O critério de estabilidade para o método explícito exige que o coeficiente do termo T m p na equação de diferenças finitas unidimensional seja zero ou positivo. Analise a situação na qual as temperatu
Deduza a equação de diferenças finitas, bidimensional e transiente, para a temperatura no ponto nodal 0 localizado sobre a fronteira entre dois materiais diferentes.
Um fino bastão com diâmetro D está inicialmente em equilíbrio com a sua vizinhança, um grande recipiente, onde há vácuo, a uma temperatura T v i z . De repente, uma corrente elétrica I ( A ) é passada
Deduza uma equação de diferenças finitas explícita para um nó interior para a condução tridimensional transiente. Também determine o critério de estabilidade. Suponha propriedades constantes e espaçam
Uma placa unidimensional com espessura 2 L está inicialmente a uma temperatura uniforme T i . Subitamente, uma corrente elétrica é passada através da placa, causando um aquecimento volumétrico uniform