Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 127
Considere um cilindro de densidade flutuando verticalmente na água , como na Figura P2.127. Deduza uma fórmula para os valores estáveis de em função de e aplique-a ao caso .
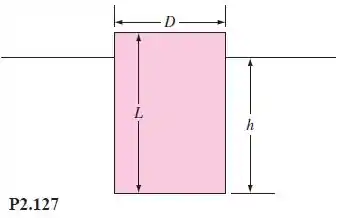
Passo 1
Fala galera, vem comigo resolver essa questão!!
Queremos aqui encontrar uma fórmula para os valores estáveis de em função de , em que esse é a densidade relativa do cilindro. Para isso, podemos começar usando a ideia de que as forças que atuam verticalmente o mantém em equilíbrio, ou seja, a soma das forças é igual a zero. Assim temos:
Passo 2
Para encontrarmos o que estamos procurando, podemos usar a formula 2.37:
Em que é o centróide, é o metacentro, é o centro de flutuabilidade, é o momento de inércia e é o volume submerso. Para um cilindro o momento de inercia é dado por:
O volume submerso para essa questão é:
Para a estabilidade de massa, temos que:
O centro de gravidade está em acima do fundo e está em acima do fundo. Para essa questão a distancia é dada por:
Passo 3
Agora que temos todos os dados, vamos substituir na equação 2.37.
Passo 4
Com o resultado encontrado, vamos aplicar para o caso onde . Assim, temos que:
Se usarmos a formula de Bhaskara, vamos encontrar que