Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 5
Considere condução de calor unidimensional, em regime estacionário, através da geometria simétrica mostrada na figura.
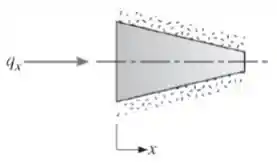
Supondo que não há geração interna de calor, desenvolva uma expressão para a condutividade térmica k(x) para as seguintes condições: e , em que está em metros quadrados, em kelvins e em metros.
Passo 1
Beleza galerinha, vamos lá! Aplicando o balanço energético, Eq. 1.12c, ao sistema, segue-se que, uma vez que
Passo 2
Usando a lei de Fourier, Eq. 2.1, com expressões apropriadas para e , produz
Resolvendo para e reconhecendo suas unidades são ,
Resposta
Exercícios de Livros Relacionados
42 – Considere um duto extenso de raio interno r 1 , raio externo r 2 e condutividade térmica k . A superfície externa do duto está sujeita à convecção como o meio a uma temperatura T ∞ e o coeficient
41 – Calor é gerado em um fio extenso de raio r 0 a uma taxa constante de e ˙ g e r por unidade de volume. O fio está coberto por uma camada isolante de plástico. Expresse a condição de contorno de fl
52 - A temperatura em uma parede plana com condutividade térmica constante e sem geração de calor varia linearmente durante a condução de calor unidimensional permanente. A afirmação continua verdadei
44 – Um contêiner é formado por duas camadas esféricas A e B em perfeito contato. Considerando que o raio da interface é r 0 , expresse as condições de contorno na interface.
43 – Considere uma casca esférica de raio interno r 1 , raio externo r 2 , condutividade térmica k e emissividade ε . A superfície externa da casca está sujeita à radiação para as superfícies ao redor