Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 91

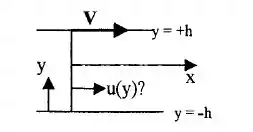
Considere o escoamento de Couette bidimensional, incompressível e permanente (escoamento entre duas placas infinitas com a placa superior se movendo a uma velocidade constante, e a inferior estacionária). Considere que o fluido é não newtoniano, com suas tensões viscosas dadas por:

τ x x = a ∂ u ∂ x c

τ y y = a ∂ v ∂ y C

τ z z = a ∂ w ∂ z c

τ x y = τ y x = 1 2 a ∂ u ∂ y + ∂ v ∂ x c

τ x z = τ z x = 1 2 a ∂ u ∂ z + ∂ w ∂ x c

τ y z = τ z y = 1 2 a ∂ v ∂ z + ∂ w ∂ y c

Em que “a” e “c” são constantes do fluido. Adote as mesmas hipóteses que foram usadas na dedução da equação (4.131). (a) Encontre o perfil de velocidade u(y). (b) Como o perfil de velocidade para este caso se compara aquele de um fluido newtoniano?

Passo 1

Tudo bem, genteee? Bora que bora encarar mais um exercício de mecflu? Só que agora temos fluidos não Newtonianos na paradaaaa!!

(a) Primeira coisa, vamos as nossas hipóteses!! Vamos negligenciar a gravidade e o gradiente de pressão. E se u = u(y) e, como temos um escoamento bidimensional, temos que u = u(u,v), porém podemos dizer que o escoamento está na direção x, temos apenas uma componente importante, que é u, logo v = 0 em ambas as paredes. Vamos começar com a equação de momento na direção x

ρ   u ∂ u ∂ x + v ∂ u ∂ y = ρ g x - ∂ p ∂ x + ∂ τ x x ∂ x + ∂ τ x y ∂ y

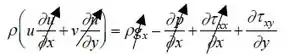
Passo 2

Vários termos são cancelados no nosso equacionamento porque v = 0 (AMÉM) e também porque τ x x = ∂ u ∂ x = 0 (porque u não varia com x, afinal, estamos em um escoamento completamente desenvolvido). Assim, temos que:

∂ τ x y ∂ y = 0

∂ τ x y ∂ y = d d y a 2 d u d y c = 0

a 2 d d y d u d y c = 0

d d y d u d y = 0

u = C 1 y + C 2

Passo 3

As condições de contorno desse belezura são as condições de não deslizamento na placa inferior e com velocidade V na placa superior!!

u y = - h = 0 → C 1 - h + C 2 = 0

u y = + h = V → C 1 h + C 2

C 1 = V 2 h

C 2 = V 2

Passo 4

Temos então que a solução para o perfil de velocidade pode ser dada como:

u y = V 2 h y + V 2

Passo 5

(b) Se tivéssemos um fluido newtoniano, você pode olhar no livro que teríamos EXATAMENTE A MESMA EQUAÇÃO!

u y = V 2 h y + V 2

Resposta

a     e   b   u y = V 2 h y + V 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma certa região de escoamento permanente, bidimensional, incompressível, o campo de velocidade é dado por V → = u , v = a x + b i → + - a y + c x j → . Mostre que essa região do escoamento pode se
Na deduaçao da equação de Bernoulli para regiões de escoamento sem viscosidade, reescrevemos a equação de Euler permanente, incompressível em uma forma mostrando que o gradiente de três termos escalar
Considere o escoamento de um fluido permanente, incompressível, bidimensional em um duto convergente, com paredes retas. A vazão em volume é V ˙ e a velocidade ocorre somente na direção radial, com ur
Em uma região irrotacional de escoamento, podemos escrever o vetor de velocidade como o gradiente da função potencial de velocidade escalar V → =∇ → ϕ . As componentes da velocidade em coordenadas cil
Água à temperatura de 20°C gira como um corpo rígido em relação ao eixo z em um recipiente cilíndrico giratório. Não há tensões viscosas pois a água move-se como um corpo sólido; portanto a equação de