Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 35

Na deduaçao da equação de Bernoulli para regiões de escoamento sem viscosidade, reescrevemos a equação de Euler permanente, incompressível em uma forma mostrando que o gradiente de três termos escalares é igual ao produto vetorial do vetor velocidade com o vetor vorticidade, observando que z está apontando verticalmente para cima:

∇ P ρ + V 2 2 + g z = V →   x   ζ →

Empregamos então alguns argumentos sobre a direção do vetor gradiente e a direção do produto vetorial de dois vetores, para mostrar que a soma dos três termos escalares deve ser constante ao longo de uma linha de corrente. Nesse problema, você usará uma abordagem diferente para obter o mesmo resultado. Isto é, considere o produto escalar de ambos os lados da equação de Euler com o vetor de velocidade e aplique algumas regras fundamentais do produto escalar de dois vetores. Desenhos podem ajudar.

Passo 1

Nosso primeiro passo vai ser fazermos exatamente o que o exercício está nos pedindo, beleza?

∇ P ρ + V 2 2 + g z . V → = V →   x   ζ → . V →

Note que o produto escalar do lado direito da equação é um vetor que é perpendicular ao vetor velocidade. Se liga no desenho abaixo, a nossa linha preta é a linha de corrente, beleza?

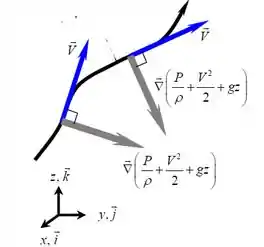
E, como a gente bem sabe, se esses caras são PERPENDICULARES entre si, por definição temos que seu valor será zero.

∇ P ρ + V 2 2 + g z . V → = 0

Passo 2

Mas note que existem três formas de deixarmos a equação acima válida, ou seja, ela ser igual a zero.

  1. ∇ P ρ + V 2 2 + g z = 0

  2. V → = 0

  3. Considerando esses dois vetores perpendiculares entre si

Vamos agora discutir um pouco sobre o que cada uma dessas opções nos diz!!!!

A opção (a) representa um caso restrito onde a quantidade entre parênteses é constante em TODOS OS LUGARES! Opção (b) é o caso “trivial” onde o fluido tá ali paradinho de boas.

(c) É o caso mais geral para trabalharmos. Mas para usarmos essa opção, a gente precisa dizer que o vetor velocidade é PARALELO em qualquer ponto de uma linha de corrente, beleza? E aí com isso a gente pode AFIRMAR que ∇ P ρ + V 2 2 + g z será perpendicular à linha de corrente (e por consequência também ao vetor velocidade).

Finalmente (UFFFAAA) a gente pode argumentar e dizer que o gradiente de um escalar é um vetor que toca perpendicularmente à uma superfície imaginária, e que, esse escalar é uma CONSTANTE! Por isso que a gente pode afirmar que :

P ρ + V 2 2 + g z = C o n s t a n t e   a o   l o n g o   d a   l i n h a   d e   c o r r e n t e

Resposta

P ρ + V 2 2 + g z = C o n s t a n t e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A componente x da velocidade em um campo de escoamento incompressível, bidimensional é dada por υ=- A x y , em que v é em m/s, as coordenadas são medidas em metros e A=1m - 1 s - 1 . Não há componente
Considere o escoamento do Problema 5.48. Avalie o módulo, direção e sentido da força resultante de pressão que age sobre aplaca superior entre ri e R, se ri = R/2.
Um campo de velocidade é dado por V → = A x 3 + B x y 2 i ^ + A y 3 + B x 2 y j ^ , A = 0,2m - 2 s - 1e B é uma constante e as coordenadas são medidas em metros. Determine o valor e as unidades de B c
Um líquido incompressível com viscosidade desprezível e massa específica ρ = 850 kg/m3 escoa em regime permanente através de um tubo horizontal. A área da seção transversal do tubo varia linearmente d
Um líquido incompressível com viscosidade desprezível e massa específica ρ = 1250 kg/m3 escoa em regime permanente através de um tubo de 5 m de comprimento com seção convergentedivergente, cuja área v