Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 20

Considere o escoamento do Problema 5.48. Avalie o módulo, direção e sentido da força resultante de pressão que age sobre aplaca superior entre ri e R, se ri = R/2.

Passo 1

Pessoal, vamos olhar a figura do problema 5.48:

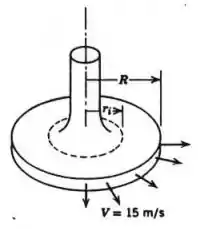
Nesta questão, vamos assumir que:

- O fluido é incompressível;

- O regime é permanente;

- Não há atrito e;

- Fluxo uniforma por toda a seção.

O enunciado pede para encontrarmos a força resultante de pressão. Vamos precisar relacionar 2 equações.

A equação geral de força:

F → = - ∫ P d A →

E a equação de Euler 6.1:

ρ g → - ∇ p = ρ D V → D t

Passo 2

Devido ao formato cilíndrico, vamos aplicar a equação de Euler na direção r, dada pela equação 6.3a do livro:

ρ a r = ρ g r - ∂ p ∂ r

Podemos simplificar para:

ρ V r d V r d r = - d p d r

No exercício 5.48, foi demonstrado que:

V r = V R r

Vamos usar esta substituição na equação de Euler:

ρ V R r   d V R r d r = - d p d r

ρ V R r - V R r 2 = - d p d r

d p d r = ρ V 2 R 2 r 3

d p = ρ V 2 R 2 r 3 d r

Para determinar a distribuição de pressão p r , vamos integrar a expressão encontrada acima:

∫ p a t m p d p = ∫ R r ρ V 2 R 2 r 3 d r

p - p a t m = ρ V 2 R 2 - 1 2 r 2 r R

p - p a t m = ρ V 2 R 2 - 1 2 r 2 + 1 2 R 2

p - p a t m = ρ V 2 R 2 2 1 R 2 - 1 r 2

Passo 3

Agora vamos voltar com a definição de força:

F → = - ∫ P d A →

No intervalo da questão ( r i = R / 2 ) , vamos ter:

F → = ∫ R / 2 R p - p a t m d A →

Em coordenadas cilíndricas, o diferencial da área é definido por:

d A = 2 π r d r

F → = ∫ R / 2 R p - p a t m 2 π r d r

Substituindo o valor de p - p a t m :

F → = ∫ R / 2 R ρ V 2 R 2 2 1 R 2 - 1 r 2 2 π r d r

F → = π ρ V 2 R 2 ∫ R / 2 R r R 2 - 1 r d r

F → = π ρ V 2 R 2 r 2 2 R 2 - ln ⁡ r R R / 2

F → = π ρ V 2 R 2 R 2 2 R 2 - R 2 8 R 2 - ln ⁡ R - ln ⁡ R 2

F → = π ρ V 2 R 2 1 2 - 1 8 - ln ⁡ R R / 2

F → = π ρ V 2 R 2 3 8 - ln ⁡ 2

F → = π ρ V 2 R 2 0,375 - 0,693

Como o enunciado não fornece o valor da massa específica do fluido, vamos deixar na forma literal:

F → = - 0,318 π ρ V 2 R 2

Resposta

F → = - 0,318 π ρ V 2 R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.79 Considere o campo de escoamento representado pela função de corrente ψ = - A / 2 x 2 + y 2 , em que A é constante. Esse é um possível escoamento bidimensional incompressível? O escoamento é irrot
5.78 Considere um campo de velocidade para um movimento paralelo ao eixo x com cisalhamento constante. A taxa de cisalhamento é du/dy=A, em que A = 0,1s - 1 . Obtenha uma expressão para o campo de vel
5.77 Considere o campo de escoamento representado pela função de corrente ψ = x 6 - 15 x 4 y 2 + 15 x 2 y 4 - y 6 . Esse é um possível escoamento bidimensional incompressível? O escoamento é irrotacio
5.80 Considere o campo de escoamento representado pela função de corrente ψ = A x y + A y 2 , em que A = 1s - 1 . Mostre que este campo de velocidade representa um possível escoamento incompressível.
5.82 Considere o campo de velocidade dado por V → = A x 2 i ^ + B x y j ^ , em que A = 3,3m - 1 s - 1 , B = - 6,6m - 1 s - 1 e as coordenadas são medidas em ft.(a) Determine a rotação do fluido.(b) Av