Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 7

Considere a esfera de raio R imersa em uma corrente uniforme U 0 , como mostra a Figura P 4.7 . De acordo com a teoria do Capítulo 8 , a velocidade do fluido ao longo da linha de corrente A B é dada por

V = u i = U 0 1 + R 3 x 3 i

Encontre (a) a posição da aceleração máxima do fluido ao longo de A B e (b) o tempo necessário para que uma partícula de fluido se desloque de A a B .

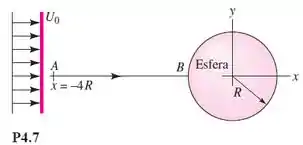
Passo 1

E aí, tudo bem? Bora matar essa questão rapidinho!

a)

Nosso campo de velocidade é unidimensional o que facilita bastante as contas. haha

Agora para encontrarmos nossa aceleração vamos derivar o campo de velocidade!

Como não temos componentes dependentes do tempo:

d u d t = u ∂ u ∂ x

d u d t = U 0 1 + R 3 x 3 .   - 3 U 0 R 3 x 4

d u d t = - 3 U 0 2 R 3 1 x 4 + R 3 x 7

Bem nossa questão nos pede a aceleração máxima, logo vamos derivar em função de x e igualar a zero, aquele velho bizu de sempre!

d u d x d u d x = 0 ; d u d x - 3 U 0 2 R 3 1 x 4 + R 3 x 7 = 0  

3 U 0 2 R 3 4 x 5 + 7 R 3 x 8 = 0

Assim vamos ter a seguinte situação!

4 x 5 + 7 R 3 x 8 = 0

Vamos isolar os termos!

7 R 3 x 8 - 1 = - 4 x 5 - 1

x 8 = - 7 R 3 x 5 4

Resolvendo pra x !

x = - 7 R 3 4 3

x = - 1,205   R

Considerando o centro da esfera a referencia do sistema cartesiano temos nosso ponto de aceleração máxima vai ficar um pouquinho a esquerda da nossa esfera:

Passo 2

b)

Bem, até agora só estávamos derivando, mas agora chegou a hora de integrar haha!

Bem, vamos organizar nossa formula da seguinte maneira:

d x d t = U 0 1 + R 3 x 3

Vamos separar nossas variáveis e integrar no limite proposto, de x = 0 até x = L , vai ficar assim:

∫ 0 L d x U 0 1 + R 3 x 3 = ∫ 0 t d t

∫ - 4 R R d x 1 + R 3 x 3 = ∫ 0 t U 0 d t

Essa integral é um pouco grandinha, então peço um pouquinho de paciência para resolvermos ela:

Primeiro vamos organizar nossas variáveis

d x 1 + R 3 x 3 = x 3 x 3 + R 3

Vamos escrever x 3 como x 3 + R 3 - R 3 :

x 3 + R 3 - R 3 x 3 + R 3 + R 3 - R 3

Separando os termos:

x 3 + R 3 x 3 + R 3 - R 3 x 3 + R 3

1 - R 3 ⋅ 1 x 3 + R 3

Agora podemos começar integrar!

∫ - 4 R - R d x 1 + R 3 x 3 = ∫ - 4 R - R d x - R 3 ∫ - 4 R - R d x x 3 + R 3

U 0 t = ∫ - 4 R - R d x - R 3 ∫ - 4 R - R d x x 3 + R 3

Agora vamos para a parte mais chatinha! Conta grandinha! kkkk

∫ - 4 R - R d x x 3 + R 3 = ∫ - 4 R - R d x x + R x 2 - R x + R 2

Aplicando a regra de decomposição e linearidade:

1 3 R 2 ∫ - 4 R - R d x x + R + 1 3 R 2 ∫ - 4 R - R x - 2 R x 2 - R x + R 2 d x

1 3 R 2 ln ⁡ x + R - 1 6 R 2 ln ⁡ x 2 - R x + R 2 + 1 3 R 2 arctg ⁡ 2 x - R 3 R 2 - 4 R - R

NOSSA, Tá grandinha a integral, agora vamos montar todas as partes dela!

U 0 t = x - 4 R - R - R ⋅ ln ⁡ x + R - 2 ln ⁡ x 2 - R x + R 2 + 2 3 arctg ⁡ 2 x - R 3 R 2 6 - 4 R - R

Agora olha só a maldade, essa conta toda nós matamos nesse termo aqui:

ln ⁡ x + R - 4 R - R → ln ⁡ 0 - ln ⁡ - 3 R

Como sabemos ln ⁡ 0 = - ∞ , logo todo esse termo fica:

U 0 t = 3 R - - ∞

t = ∞

Meia hora de conta pra saber que o tempo para chegar no ponto de estagnação é infinito!

Isso é tudo pessoal, conseguimos mais uma! \o/

Sem panda feliz nessa questão hahaha!

Resposta

a)

x = - 1,205   R

b)

t = ∞

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação cúbica de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U , na b
Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação parabólica de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U ,
5.21 Para um escoamento incompressível no plano r θ , a componente r da velocidade é dada por V r = - Λ cos ⁡ θ / r 2 . Determine uma possível componente θ da velocidade. Quantas possíveis componentes
5.15 A componente y da velocidade em um campo de escoamento em regime permanente e incompressível, no plano x y , é v = B x y 3 , em que B = 0,2m - 3s - 1 e x e y são medidos em metros. Encontre a mai
5.19 Quais dos seguintes conjuntos de equações representam possíveis casos de escoamento incompressível?(a) V r = - K / r ; V θ = 0 (b) V r = 0 ; V θ = K / r (c) V r = - K cos ⁡ θ / r 2 ; V θ = - Ks e