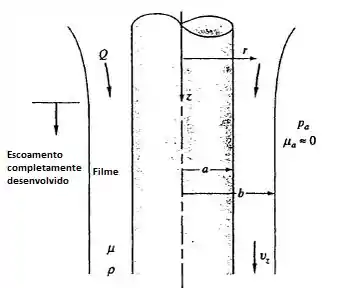
Considere um filme viscoso de líquido escoando uniformemente pelo lado de uma haste vertical de raio a, como na figura abaixo. Em algum ponto abaixo na haste o filme se aproximará de um escoamento drenante terminal ou totalmente desenvolvido de raio externo b constante, com . Considere que a atmosfera não oferece resistência de cisalhamento ao movimento do filme. Deduza uma equação diferencial para , defina as condições de contorno apropriadas e resolva a distribuição de velocidade do filme. Como o raio b do filme se relaciona com a vazão volumétrica Q total do filme?
Passo 1
Tudo bem, genteee?!! Então, vamos começar nossas aventuras com a mecânica dos fluidos? Olha que maneiro!!! O enunciado já disse pra gente qual será a coordenada de interesse para termos o perfil de velocidade, certo? Ele disse pra gente que será a componente z a importante. Além disso, ele disse que nosso escoamento é completamente desenvolvido, o que indica que o perfil de velocidade não vai mais variar na direção do escoamento, em outras palavras, . Além disso, vamos considerar regime estacionário, ou seja, .
Vamos olhar primeiro a equação da continuidade e considerar um fluido incompressível, ou seja, densidade constante!!!
A equação de Navier Stokes em coordenadas cilíndricas é:
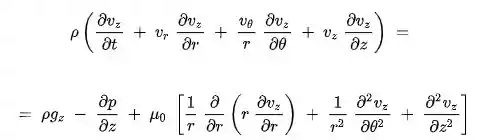
Passo 2
Com nossas simplificações, incluindo aquela que encontramos como resultado da equação da continuidade ao final temos algo do tipo:
Vamos integrar essa belezinha?
Passo 3
As condições de contorno desse belezura nos dizem que em (condição de não deslizamento) e que para encontrar nossas constantes!!
Passo 4
Para encontrarmos a vazão volumétrica, precisamos integrar o perfil de velocidade em torno da seção transversal que está ocorrendo o escoamento. Bem, aqui será uma integral dupla pois precisamos variar o raio de escoamento e o ângulo que estamos capturando. Percebemos que nossa equação de perfil de velocidade não depende do ângulo, mas somente do raio, então ao fazermos a integral dupla, e integrarmos em teremos já um fator , certo?