Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 22
Um campo de escoamento no plano xy é descrito por . Converta essas velocidades em coordenadas polares planas, e .
Passo 1
Falaaaaaaaaeeeeeeeeeeeee, tamo aqui de novo! Bora lá resolver essa ai!
Bora fazer um esqueminha com essas velocidades pra gente conseguir essas coordenadas, temos que para conseguir a velocidade V, temos de ter as duas componentes dela, certo, a partir daí, chegaremos em:
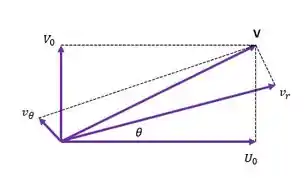
Veja que V também é um “reflexo” de e .
Passo 2
Pô, e agora?! Cara, vamos usar a boa e velha geometria e umas relações trigonométricas, bora! Teremos que:
e
Resposta
Exercícios de Livros Relacionados
Óleo viscoso da figura abaixo é posto em movimento permanente por um cilindro interno concêntrico movendo-se axialmente à velocidade U dentro de um cilindro externo fixo. Considerando pressão e massa
Dada a distribuição de velocidade permanente, incompressível, V = 3 x i + 0 j + C y k , em que C é uma constante, se o escoamento é irrotacional, o valor de C deverá ser33/20-3/2-3
Dada a distribuição de velocidade permanente, incompressível, V = 3 x i + C y j + 0 k , em que C é uma constante, se a conservação da massa for satisfeita, o valor de C deverá ser:33/20-3/2-3
A two-dimensional, incompressible flow has the velocitycomponents u 5 4y and v 5 2x. (a) Find the accelerationcomponents. (b) Is the vector acceleration radial? (c) Sketcha few streamlines in the firs
For laminar flow between parallel plates (see Fig. 4.12b),the flow is two-dimensional (υ ? 0) if the walls areporous. A special case solution is u 5 (A 2 Bx)(h2 2 y2),where A and B are constants. (a)