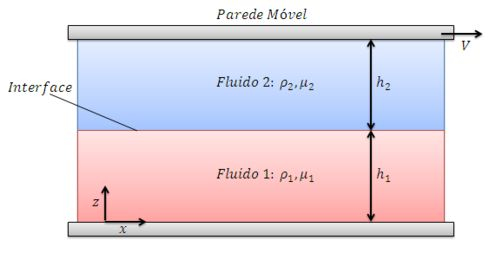
Considere a forma modificada do escoamento Couette na qual há dois líquidos imiscíveis entre duas placas planas, paralelas e infinitamente longas (Figura ). O escoamento é permanente, incompressível, paralelo e laminar. A placa superior se move a uma velocidade para a direita, e a placa inferior está estacionária. A gravidade age na direção (para baixo na figura). Não há gradiente de pressão empurrando os fluidos através do canal – o escoamento se estabelece somente pelos efeitos viscosos criados pela placa superior em movimento. Você pode ignorar os efeitos da tensão superficial e considerar que a interface seja horizontal. A pressão na parte inferior do escoamento () é .

(a) Liste todas as condições de contorno apropriadas de velocidade e pressão.

(b) Resolva para o campo de velocidade.

(c) Resolva para o campo de pressão.

(d) Seja o fluido a água e o fluido óleo novo de motor, ambos a . Faça também , e . Desenhe o gráfico de como uma função de através de todo o canal. Discuta os resultados.

Agora que listamos as condições de contorno vamos para o item (b). Devemos obter o perfil de velocidades. Para isso, vamos analisar os dois fluidos separadamente.

Começando pelo fluido , nosso primeiro passo para encontrar o perfil de velocidade é aplicar a equação da continuidade para coordenadas cartesianas:

Assumindo que estamos em regime permanente e, que como mencionamos no item (a) apenas a componente da velocidade é não-nula:

Nossa equação se reduz à:

Então, concluímos que não depende da direção . Ou seja:

Nosso próximo passo para obter o perfil de velocidade será aplicar a equação de Navier-Stokes.

Como só temos velocidade na direção , vamos aplicar a equação de Navier-Stokes para esta componente:

Vamos agora analisar cada termo da equação. Começando pelo lado esquerdo, estamos considerando um processo em regime estacionário e que as componentes de velocidade e são nulas. Além disso, vimos pela equação da continuidade que . Então:

E o lado esquerdo da equação fica:

Vamos agora olhar os termos do lado direito.

Como mencionamos no item (a), não há gradiente de pressão na direção e, a gravidade atua apenas no sentido de . Além disso, também vimos que , então:

A equação de Navier-Stokes se reduz à:

Como a segunda derivada em relação a é nula, podemos dizer que:

Em que é uma constante. Integrando com relação à :

Aplicando a primeira condição de contorno:

E o perfil fica:

Antes de obter vamos determinar o perfil de velocidade do fluido .

Para chegar ao perfil de velocidades do fluido , nosso primeiro passo é aplicar a equação da continuidade para coordenadas cartesianas:

Como estamos em regime permanente e, apenas a componente da velocidade é não-nula:

Nossa equação se reduz à:

Então, concluímos que não depende da componente . Ou seja:

Nosso próximo passo para obter o perfil de velocidade será aplicar a equação de Navier-Stokes.

Como só temos velocidade na direção , iremos aplicar a equação de Navier-Stokes apenas para esta componente:

Vamos novamente analisar cada termo da equação. Começando pelo lado esquerdo, temos um processo em regime estacionário e as componentes de velocidade e são nulas. Além disso, vimos pela equação da continuidade que . Então:

E o lado esquerdo da equação se reduz à:

Vamos agora olhar os termos do lado direito.

Não temos gradiente de pressão na direção e, a gravidade atua apenas no sentido de . Além disso, , então:

E a equação de Navier-Stokes é reduzida para:

Como a segunda derivada em relação a é nula, podemos dizer que:

Em que é uma constante. Integrando com relação à :

Aplicando as condições de contorno:

Subtraindo a segunda equação da primeira:

Substituindo na primeira relação:

Aplicando e no perfil :

Resta ainda obter . Para isso, vamos aplicar a condição de contorno em relação à tensão superficial na interface:

Substituindo nos perfis de velocidade e :

Vamos agora para o item (c). Neste item devemos obter o perfil de pressão entre as placas.

Para isso, vamos seguir a mesma estratégia do item (b) e analisar cada fluido separadamente. Começando pelo fluido vamos aplicar a equação de Navier-Stokes para a componente :

Vamos analisar o lado esquerdo da equação. Como :

Então, o lado esquerdo se resume à:

Vamos agora para o lado direito da equação. A gravidade atua no sentido e a componente da velocidade é nula. Então:

Então, a equação de Navier-Stokes fica:

Integrando em relação à :

Pelas condições de contorno sabemos que . Então:

Aplicando esta constante no perfil:

Vamos agora determinar o perfil de pressão no segundo fluido. Para isso, também começamos aplicando a equação de Navier-Stokes para a componente no fluido :

Vamos analisar o lado esquerdo da equação. Como vimos no item (b), :

Então, o lado esquerdo é reduzido para:

Vamos agora para o lado direito da equação. A gravidade atua no sentido e a componente da velocidade é nula. Então:

Então, a equação de Navier-Stokes fica:

Integrando em relação à :

Pelas condições de contorno sabemos que . Então:

Substituindo no perfil de :

Para encerrar, vamos para o item (d). Temos que o fluido é água e o fluido é óleo novo de motor, ambos a . Sabendo também que , e devemos desenhar o gráfico de . Vamos lá?

Antes de ir para o gráfico, vamos encontrar as respectivas viscosidades (Tabelas e , apêndice A):

A partir das nossas equações de perfil e, aplicando para diferentes valores de :

Com o auxílio de Excel, devemos chegar em uma função da forma:

Pela análise do perfil de velocidades podemos ver que na camada de óleo a velocidade praticamente se mantém constante em , enquanto na camada de água podemos ver que ocorre uma grande variação da velocidade, mesmo que .

Isso acontece porque há uma grande diferença de viscosidade entre os fluidos, com . Por ser menos viscosa a água dissipa mais facilmente a energia de quantidade de movimento, enquanto o oposto acontece na camada de óleo de motor.