Considere geração uniforme de energia térmica no interior de uma parede unidimensional de espessura , com uma superfície mantida a e a outra superfície isolada termicamente.
(a) Determine uma expressão para o fluxo térmico condutivo para a parede fria e para a temperatura da parede quente , expressando os seus resultados em termos de , , e .
(b) Compare o fluxo térmico encontrado na parte (a) com o fluxo térmico associado a uma parede plana sem geração de energia, cujas temperaturas superficiais estão a e .
Passo 1
Para resolver essa questão, vamos considerar o seguinte esquema de uma parede plana com geração de calor.
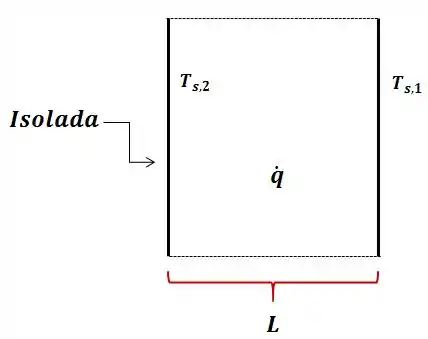
PRESSUPOSTOS:
(1) Condições em estado estacionário;
(2) Propriedades constantes;
(3) Transferência de calor unidimensional;
(4) Geração volumétrica uniforme.
Passo 2
(a) Temos que a equação geral para transferência de calor pode ser escrita da seguinte maneira:
Aqui, é a temperatura na direção de , é a taxa de transferência de calor, é a condutividade térmica da parede, é à distância ao longo da parede na direção vertical e e são constantes arbitrárias.
Passo 3
Queremos encontrar e para isso, podemos usar as condições de contorno. A primeira condição se dá ao fato de que uma das superfícies da parede está isolada. A expressão de fluxo térmico condutivo é a seguinte.
Para , não a fluxo devido ao isolamento. Assim
Agora vamos usar a segunda condição de contorno. Quando , temos que . Assim temos que:
Assim, temos que a equação de distribuição de temperatura é:
Passo 4
Para encontrar uma equação que represente a temperatura , podemos substituir na função acima. Assim temos:
Podemos encontrar uma expressão para o fluxo térmico condutivo para a parede fria usando a equação de distribuição de temperatura e expressão de fluxo térmico quando . Assim temos:
Portanto a expressão para o fluxo térmico condutivo para a parede fria é:
Passo 5
(b) Para uma parede plana sem geração de energia, a distribuição de temperatura é dada pela equação 3.3. Assim, temos o seguinte:
Podemos encontrar uma expressão para o fluxo térmico condutivo para a parede Da seguinte maneira:
Portanto a expressão para o fluxo térmico condutivo para a parede:
Resposta
(a)
(b)