Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 92
No Problema 3.79, a fita aquecedora atua como um protetor contra as perdas de calor da parede para o exterior e o fluxo térmico necessário para tal depende de condições operacionais na câmara, tais como e . Como uma primeira etapa no projeto de um controlador para o aquecedor protetor, calcule e represente graficamente e em função de para e ; e .
Passo 1
Fala Galera!!
Para resolver essa questão, vamos precisar dos seguintes dados fornecidos no enunciado da questão 3.79.
DADOS FORNECIDOS:
Temperatura do ar no interior da câmara: ; e
Temperatura externa:
Coeficiente convectivo externo:
Coeficiente convectivo no interior da câmara:
Espessura da parede:
Condutividade térmica da parede:
Geração volumétrica de calor:
PRESSUPOSTOS:
(1) condições de estado estacionário;
(2) condução unidimensional;
(3) geração volumétrica uniforme;
(4) propriedades constantes.
Passo 2
Podemos fazer o seguinte esquema do processo:
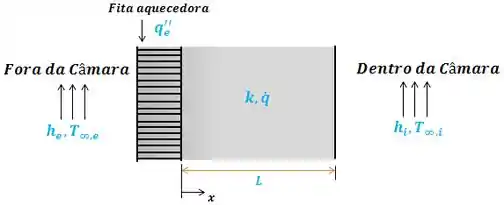
Se nenhum calor gerado dentro da parede for perdido para o exterior da câmara, o gradiente na posição deve ser zero. Como é uniforme, a distribuição de temperatura deve ser parabólica. Assim, podemos escrever a solução geral para a condução de calor em estado estacionário com geração interna de calor em uma parede plana.
Aqui, é o calor interno gerado na parede, é a condutividade térmica da parede plana e e são as constantes de integração. Queremos encontrar e , para isso, podemos aplicar as condições de contorno.
Passo 3
A primeira condição de contorno na câmara externa onde não a perde de calor para fora da câmara, portando
Aqui, é a condutividade térmica da parede plana. Aplicando a condição de contorno na equação 1 temos o seguinte:
Passo 4
A segunda condição de contorno na câmara interna é a seguinte:
Aqui, é o coeficiente de transferência de calor, é a temperatura da água e é a temperatura quando . Aplicando a condição de contorno na equação 1 temos o seguinte:
Assim, temos que a equação 1 se torna a seguinte:
Passo 5
Agora, podemos calcular o fluxo de calor a ser fornecido pela fita aquecedora usando a equação geral do balanço energético da parede plana. Como o calor gerado pela fita tem que ser igual ao calor perdido pela convecção do ar externo com a parede, assim, podemos dizer o seguinte:
Aqui, é o coeficiente de transferência de calor da câmara externa, é a temperatura da parede plana em e é a temperatura do ar ambiente na câmara externa. Substituindo na equação acima, temos:
Substituindo os termos da equação acima e deixando ela em função de e , temos o seguinte:
Passo 6
Com a equação encontrada no passo anterior, podemos calcular o fluxo de calor variando em função da temperatura interna câmara e da geração volumétrica de calor na parede . Fixando e variando de a , podemos produzir a seguinte tabela de dados.
Fixando e variando de a , podemos produzir a seguinte tabela de dados.
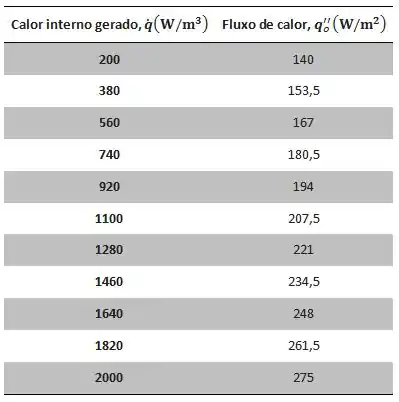
Fixando e variando de a , podemos produzir a seguinte tabela de dados.
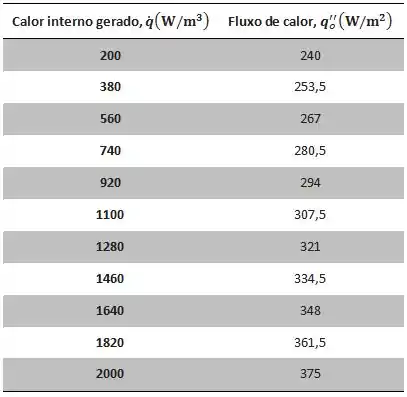
Passo 7
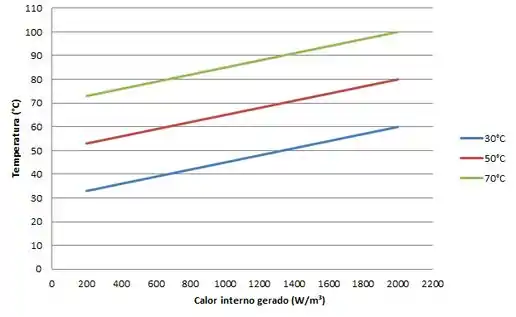
Com os dados tabelados acima, podemos plotar o seguinte gráfico para o fluxo de calor em função da taxa de geração de calor e da temperatura no interior da câmara.
Passo 8
Agora, queremos plotar o gráfico da temperatura da parede plana quando . Para isso vamos usar a equação que encontramos no passo 4. Assim temos:
Substituindo Temos o seguinte:
Agora, podemos substituindo os termos da equação acima pelos dados fornecidos e deixando ela em função de e , temos o seguinte:
Passo 9
Com a equação encontrada no passo anterior, podemos calcular temperatura em variando em função da temperatura interna câmara e da geração volumétrica de calor na parede . Fixando e variando de a , podemos produzir a seguinte tabela de dados.
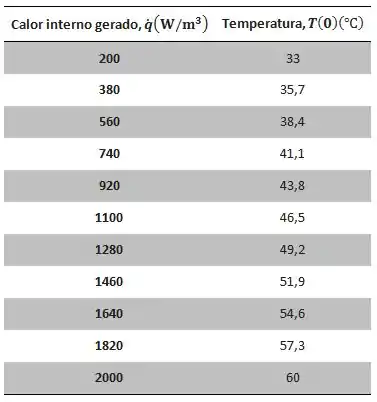
Fixando e variando de a , podemos produzir a seguinte tabela de dados.
Fixando e variando de a , podemos produzir a seguinte tabela de dados.
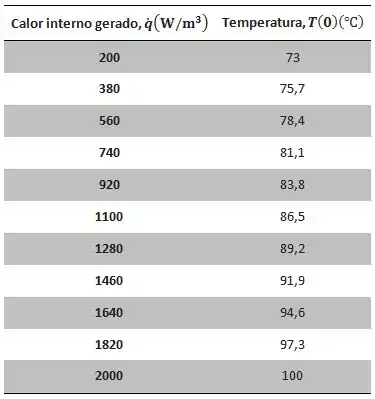
Passo 10
Com os dados tabelados acima, podemos plotar o seguinte gráfico para a temperatura da parede plana quando em função da taxa de geração de calor e da temperatura no interior da câmara.
