Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 141
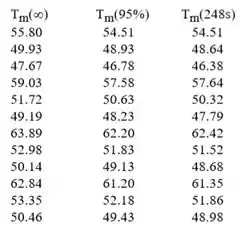
Considere o sistema do Problema 4.86. Inicialmente, a placa cerâmica () se encontra a uma temperatura uniforme de . Subitamente, os elementos elétricos de aquecimento são energizados. Usando o método implícito de diferenças finitas, calcule o tempo necessário para que a diferença entre as temperaturas superficial e inicial atinja do seu valor em condições de regime estacionário. Utilize um incremento de tempo de .
Passo 1
Vamos lá gente!! A grelha para o elemento de simetria acima é composta por nós. Os nós são pontos numa superfície com convecção; os nós são nós interiores; o nó 7 é um caso especial com geração interna e por causa da simetria, . As suas equações de finitedifference são derivadas da seguinte forma
Passo 2
Dividir por , usar as seguintes definições e reagrupar para obter as equações de diferença finita.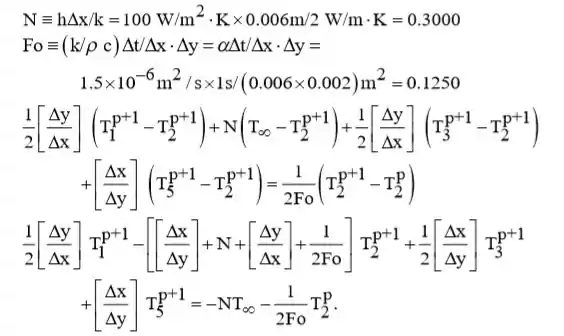 
Passo 3
Substituindo por valores numéricos, temos:
Usando a definição de Fourier e reagrupando, formando:
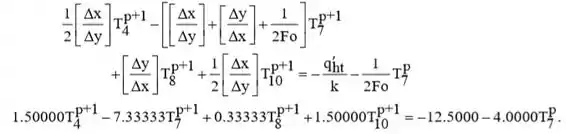
Gerando,
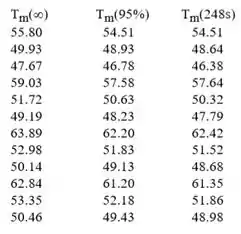
Resposta
