Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 139

Duas barras muito longas (na direção normal à página) com as distribuições iniciais de temperaturas mostradas na tabela, devem ser soldadas lateralmente uma à outra. No tempo t   =   0 , a face equivalente a m   =   3 da barra de cobre puro é colocada em contato com a face m   =   4 da barra de aço (AISI 1010). A solda atua como uma camada interfacial com espessura desprezível e resistência de contato efetiva R t , c ' ' =   2   ×   10 - 5   m 2 · K / W .

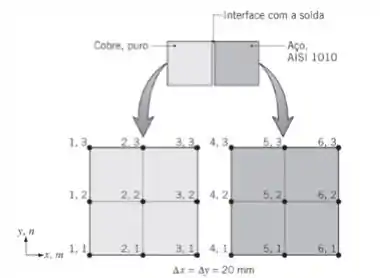
(a)Deduza a equação de diferenças finitas, utilizando o método explícito, em termos de F o e B i c = Δ x /   ( k R ' ' t , c ) para T 4 , 2 e determine o critério de estabilidade correspondente.

(b)Usando Fo = 0,01; determine T4,2 um incremento de tempo após o contato entre as duas superfícies ter sido feito. Qual o valor de Δt? O critério de estabilidade é satisfeito?

Passo 1

Vamos lá gente!! (a) A partir de um balanço energético sobre o volume de controle,

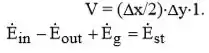
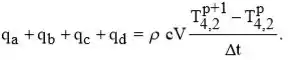
Note que enquanto q a = ( Δ T / R t , c ' ' ) A _ c   os restantes q i são termos de condução,

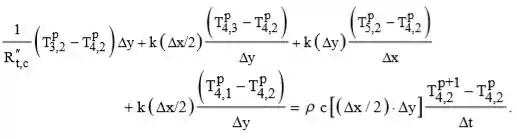
Definindo números de Fourier adequado, temos:

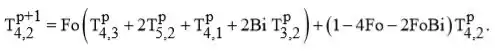
Passo 2

O critério de estabilidade exige que o coeficiente do termo T 4,2 p seja zero ou positivo,

Passo 3

Continuando, no item (b) temos que para F o = 0.01 e,

Temos,

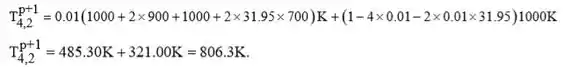
No qual,

Resposta

a )  

b ) Δ t = 1.17   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma parede plana ( ρ=4000k g / m 3,c p=500J / ( k g·K ) ,k=10W / ( m·K ) ) , com espessura L=20m m , tem inicialmente uma distribuição de temperaturas estacionária linear, com as superfícies mantidas
A superfície superior de uma placa, incluindo os seus sulcos, é mantida a uma temperatura uniforme T 1=200 ° C . A superfície inferior se encontra a T 2=20 ° C . A condutividade térmica da placa é de
Uma fábula antiga descreve como um navio de madeira foi destruído por soldados que refletiram luz do sol nos seus escudos de bronze polido sobre o casco, fazendo o navio ficar em chamas. Para testar a
Seja o domínio bidimensional mostrado. Todas as superfícies estão isoladas a menos das superfícies isotérmicas em x = 0 e L. Use uma análise unidimensional para estimar o fator de forma S.Estime o fat
O fator de forma para a condução através do canto formado por duas paredes adjacentes, com D L 5 , sendo D e L a profundidade e a espessura da parede, respectivamente, é mostrado na Tabela 4.1. O elem