Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 140

Considere o sistema do Problema 4.92. Inicialmente, sem o escoamento dos gases de exaustão, as paredes () se encontram a uma temperatura uniforme de . Usando o método implícito de diferenças finitas com um incremento de tempo de 1 h, determine as distribuições de temperaturas na parede transcorridas 5, 10, 50 e 100 horas do início da passagem dos gases de exaustão.

Passo 1

Vamos lá gente!! Realizando uma análise nodal para o IHT, temos para os nos 17 a 21:

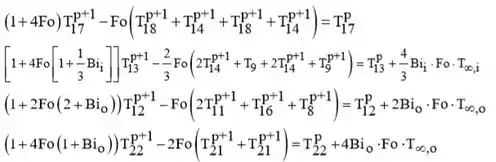
Os valores numéricos para os parâmetros relevantes são:

Passo 2

O sistema de FDEs pode ser representado em notação matricial, [A][T] = [C]. A matriz de coeficiente [A] e termos para a matriz do lado direito [C] são dados:

Para este problema foi usado um programa de computador de estoque para obter a matriz de solução

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bastão de tantálio, com 3m m de diâmetro e comprimento de 120m m , é sustentado por dois eletrodos no interior de um grande recipiente onde há vácuo. Inicialmente, o bastão está em equilíbrio com o

Placas de circuito impresso são empilhadas e tratadas pelo aquecimento sob alta pressão, como ilustrado no Problema 5.45 e descrito posteriormente no Problema 5.46. Busca-se uma solução pelo método de

Um bastão de sustentação ( k = 15W / ( m · K ) , α = 4,0 × 10 - 6m 2 / s ), com diâmetro D = 15m m e comprimento L = 100m m , atravessa um canal cujas paredes são mantidas a uma temperatura de T b = 3

Seja o elemento combustível do Exemplo 5.11, que opera a uma taxa volumétrica de geração uniforme de 1 = 107 W/m3, até que a taxa de geração mude subitamente para 2 = 2 × 107 W/m3. Use o software de e