Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 133

Um bastão de tantálio, com 3   m m de diâmetro e comprimento de 120   m m , é sustentado por dois eletrodos no interior de um grande recipiente onde há vácuo. Inicialmente, o bastão está em equilíbrio com os eletrodos e com a sua vizinhança, que são mantidos a 300   K . Subitamente, uma corrente elétrica, I   =   80   A , é passada através do bastão. Considere a emissividade do bastão igual a 0,1 e a resistividade elétrica igual a 95 × 10 - 8   Ω · m . Utilize a Tabela A.1 para obter as outras propriedades termofísicas necessárias para a sua solução. Use um método de diferenças finitas com um incremento espacial de 10   m m .

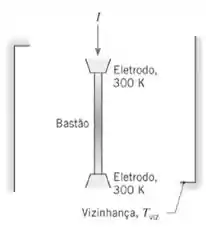
(a)Calcule o tempo necessário para o ponto na metade do comprimento do bastão atingir 1000   K .

(b)Determine a distribuição de temperaturas no regime estacionário e calcule, aproximadamente, quanto tempo será necessário para atingir essa condição.

Passo 1

Beleza galerinha, vamos lá! Nessa questão, trabalhamos com uma resistividade elétrica muito baixa, por causa disso, o tempo que vamos calcular no item a) vai acabar sendo estimado com base na equação da diferença finita. Mas não se preocupem, vai dar certo! Então chega de papo e simbora! (a)A equação de diferença finita é dada por:

T m p + 1 = F o T m - 1 p + T m + 1 p + 1 - 2 F o T m p - ε P σ Δ x 2 k A c F o T m 4 , p - T s u p 4 + I 2 ρ e Δ x 2 k A c 2 ⋅ F o

E esse monstro tem algumas coisas que já sabemos, como por exemplo:

F o = α Δ t Δ x 2

A c = π D 2 / 4  

P = π D

Passo 2

Continuando, temos que aplicar o critério de estabilidade, para podermos achar um valor de t em função de p . Portanto, vamos considerar F o = 1 2 e aplicar os valores numéricos dessa porrada de constante que temos aí em cima! Podemos achar elas no final do livro, como também no começo do capítulo 5!

T m p + 1 = F o T m - 1 p + T m + 1 p + 1 - 2 F o T m p - ε P σ Δ x 2 k A c F o T m 4 , p - T s u p 4 + I 2 ρ e Δ x 2 k A c 2 ⋅ F o

T m p + 1 = 1 2 T m - 1 p + T m + 1 p - 0.1 × 5.67 × 10 - 8 W m 2 ⋅ K 4 × 0.01 m 2 ⋅ 4 58.8 W m ⋅ 0.003 m ⋅ 1 2 T m 4 , p - 300 K 4 + 80   A 2 × 95 × 10 - 8 Ω ⋅ m   0.01 m 2 58.8 W m ⋅ K π 0.003 m 2 4 2 ⋅ 1 2

Resolvendo para T m p + 1 , temos:

T m p + 1 = 1 2 T m - 1 p + T m + 1 p - 6.4285 × 10 - 12   T m 4 , p + 103.53

Note que esta forma se aplica aos nós de 0   a 5 . Para nó 0 , T m - 1 = T m + 1 = T 1 . Como F o = 1 / 2 , usando o que já achamos para o valor do Fourier, usamos que,

Δ t = Δ x 2 F o α = 0.01 m 2 × 1 2 2.410 × 10 - 5 m 2 / s = 2.07   s

Aplicando para a equação tempo versus pressão,

t = p Δ t = 2.07 p

Passo 3

Você pode estar pensando que horas a gente vai começar a dar o valor direto do bastão a 1000 K , mas calma. Vamos fazer de uma forma mais legal ainda. Para estimar o tempo necessário para que o comprimento médio atinja 1000 K , ou seja, T o = 1000 K , vamos fazer a solução de marcação prévia começando com T i = 300 K a p = 0 . A portanto, vamos tabular esses valores, variando o valor de P .

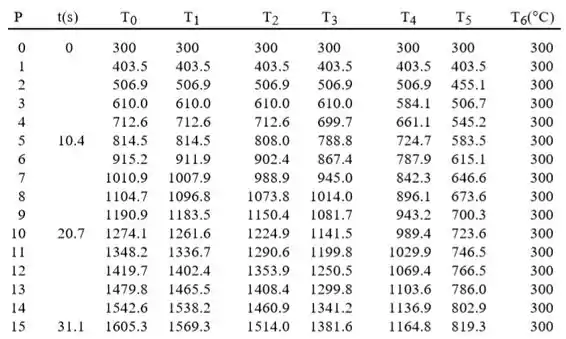
Ou seja, em p ≈ 6.9 , ou t = 6.9 × 2.07 = 14.3   s , que alcança a temperatura de T o = 1000 k

Passo 4

(b) A distribuição de temperatura em estado estacionário pode ser obtida através da solução de marcha até que apenas pequenas mudanças em T m sejam notadas. Da tabela acima, note que a p = 15 ou t = 31 s , a distribuição de temperatura ainda está mudando com o tempo. É provável que sejam necessários pelo menos mais 15 conjuntos de cálculo para ver se o estado estacionário está sendo abordado. Mas fazendo mais 15 iterações dessa com auxílio de softs, temos que,

t = 75.4   s ,     T o = 2003   K

Resposta

a ) t = 14.3   s

b ) t = 75.4   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja uma longa barra com seção transversal quadrada (0,8 m de lado) e condutividade térmica de 2 W m K . Três laterais da barra são mantidas a uma temperatura uniforme de 300°C. A quarta superfície es
Uma análise por diferenças finitas, em condições de regime estacionário, foi efetuada em uma aleta cilíndrica com um diâmetro de 12 mm e condutividade térmica de 15 W m K . O processo de transferência
Considere uma aleta plana triangular, bidimensional, com comprimento L = 50 mm e espessura na base de t = 20 mm. A condutividade térmica da aleta é k=25 W m K . A temperatura de sua base é T b=50 ° C
Seja a condução bidimensional, em regime estacionário, em uma seção transversal quadrada com temperaturas superficiais especificadas. Determine as temperaturas nos nós 1, 2, 3 e 4. Estime a temperatur
Uma folha metálica delgada, com espessura 0,25 mm e um padrão de orifícios extremamente pequenos, serve como uma grade de aceleração para controlar o potencial elétrico de um feixe de íons. Tal grade