Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 142
Seja o elemento combustível do Exemplo 5.11, que opera a uma taxa volumétrica de geração uniforme de 1 = 107 W/m3, até que a taxa de geração mude subitamente para 2 = 2 × 107 W/m3. Use o software de elementos finitos FEHT uma rotina gerada com base na abordagem via elementos finitos para obter os resultados a seguir.
(a) Calcule a distribuição de temperaturas 1,5 s depois da mudança na potência de operação e compare os seus resultados com aqueles apresentados na tabela do exemplo. Sugestão: Primeiro determine a distribuição de temperaturas no regime estacionário para 1, que representa a condição inicial para a distribuição de temperaturas transiente após a mudança degrau na potência para 2. A seguir, no menu Setup, acesse Transient na caixa Specify/Internal Generation mude o valor para 2, e no comando Run, selecione Continue (não Calculate). Veja o menu do Run na seção Help do FEHT para informações dos fundamentos na opção Continue.
(b) Use o seu modelo FEHT para representar os históricos das temperaturas no plano central e na superfície para 0 ≤ t ≤ 400 s. Quais são as temperaturas no regime estacionário e, aproximadamente, quanto tempo leva para o novo estado de equilíbrio ser atingido após o degrau na potência de operação?
Passo 1
Vamos lá gente!! Usando FEHT, um contorno do elemento de combustível é traçado com 10 mm de espessura no sentido x e comprimento arbitrário no sentido y. As condições-limite são especificadas da seguinte forma: nos planos y e no plano x = 0, tratar como adiabático; no plano x = 10 mm, especificar a opção de convecção. Especifique as propriedades do material e a geração interna com 1 q . No menu Setup, clique em Steady-state, e depois Run para obter a distribuição de temperatura correspondente à distribuição inicial de temperatura,
(a) A distribuição de temperatura 1,5 s após a mudança na potência de operação da análise FEHT e da análise FDE no Exemplo são tabeladas abaixo.,
O espaçamento da malha para a análise FEHT foi de 0,5 mm e o incremento de tempo foi de 0,005 s. Para as análises FDE, os incrementos de espaço e tempo foram de 2 mm e 0,3 s. A concordância entre os resultados dos dois métodos numéricos está dentro de .
Passo 2
(b) Usando o código FEHT, os históricos de temperatura no plano médio (x = 0) e a superfície (x = L) são traçados em função do tempo.
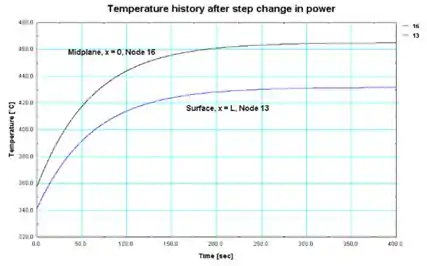
A partir da distribuição, a condição de estado estacionário (baseada em 98% de mudança) é abordada em 215 s. As distribuições de temperatura em estado estacionário após a mudança de patamar de potência da análise FEHT e FDE no Exemplo são tabeladas abaixo. A concordância entre os resultados dos dois métodos numéricos está dentro de .
Resposta
Ei, a resposta está no passo a passo :)