Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 134
Um bastão de sustentação ), com diâmetro e comprimento , atravessa um canal cujas paredes são mantidas a uma temperatura de . Subitamente, o bastão é exposto a um escoamento cruzado de gases quentes com e As paredes do canal são resfriadas e permanecem a .
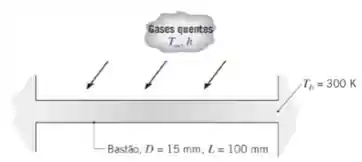
(a) Usando uma técnica numérica apropriada, determine a resposta térmica do bastão ao aquecimento por convecção. Represente graficamente a temperatura no ponto central do bastão como uma função do tempo. Usando um modelo analítico apropriado para o bastão, determine a distribuição de temperaturas no regime estacionário e compare o resultado com o obtido numericamente para um longo período de tempo.
(b) Após o bastão ter atingido condições de regime estacionário, o escoamento dos gases quentes é subitamente interrompido e o bastão resfria-se por convecção natural para o ar ambiente a e por radiação com uma grande vizinhança a . O coeficiente de transferência de calor por convecção natural pode ser estimado pela expressão , com e . A emissividade do bastão é igual a . Determine a resposta térmica do bastão nesta nova condição. Represente graficamente a temperatura no ponto central do bastão em função do tempo de resfriamento e determine o tempo necessário para o bastão atingir uma temperatura segura para o toque de .
Passo 1
Questão de software (amo???) hahahaha! Mas a questão deixa bem em aberto qual técnica numérica a gente pode usar... então vai de Excel até Matlab. Eu vou usar o IHT. Mas não se preocupem, o fundamento que vamos usar é bem fácil.
Passo 2
(a) As equações de diferenças finitas para a malha de 10 nós mostrada acima podem ser obtidas usando a Equação de Diferenças Finitas IHT, One-Dimensional, Ferramenta de Superfícies Estendidas Transientes. O histórico de temperatura-tempo para a posição de midspan T10 é mostrado no gráfico abaixo. A distribuição de temperatura em estado estacionário para a haste pode ser determinada a partir da Eq. 3.80, Caso B, Tabela 3.4. Em outros softs, vamos pegar um gráfico com métodos analíticos e numéricos, ao mesmo tempo que variamos as temperaturas e as posições, para fazermos uma curva!
A comparação é excelente, indicando que a malha nodal é suficientemente fina para obter resultados precisos.
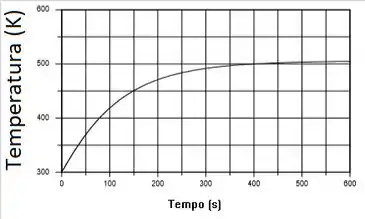
A comparação é excelente, indicando que a malha nodal é suficientemente fina para obter resultados precisos.
Passo 3
Para o gráfico do próximo item, temos que (b) A mesma abordagem de diferença finita pode ser usada para modelar o processo de resfriamento. Na utilização da ferramenta IHT, foi utilizado o seguinte procedimento: (1) Configurar os FDEs com o coeficiente de convecção expresso como , a soma dos coeficientes de convecção livre e de radiação linearizada com base na temperatura nodal .
Para uma solução inicial, temos que . Aplicando isso para o gráfico de resfriamento, temos um para a temperatura de ,
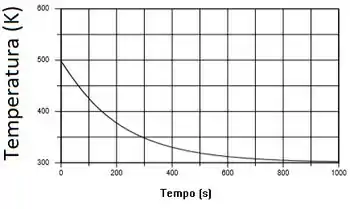
Resposta
Ei, a resposta está no passo a passo :)