Placas de circuito impresso são empilhadas e tratadas pelo aquecimento sob alta pressão, como ilustrado no Problema 5.45 e descrito posteriormente no Problema 5.46. Busca-se uma solução pelo método de diferenças finitas, com duas considerações adicionais. Em primeiro lugar, o livro deve ser tratado como tendo características distribuídas no espaço, em vez de agrupadas, através do uso de um espaçamento de malha de , com os nós nos centros das placas de circuito ou das chapas. Em segundo lugar, em vez de aquecer subitamente as placas de suporte até a temperatura de , o procedimento de aquecimento adotado é o mostrado a seguir, com o objetivo de minimizar tensões térmicas excessivas induzidas pela rápida mudança nos gradientes de temperatura nas proximidades das placas de suporte.

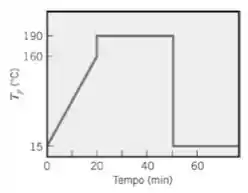
(a) Usando um incremento de tempo de e o método implícito, ache o histórico da temperatura no plano central do livro e determine se a cura ( por ) irá ocorrer.

(b) Após a redução da temperatura das placas de suporte para ), quanto tempo será necessário para que a temperatura no plano central do livro atinja , uma temperatura segura na qual o operador pode começar o descarregamento da prensa?

(c) Valide o seu código computacional usando um procedimento de aquecimento com uma mudança súbita da temperatura da placa de suporte de para e compare os resultados com os obtidos com uma solução analítica apropriada (veja o Problema 5.46).

Legal? Vamos continuar então. A equação de diferença finita para o nó de placa () ao lado do vidro segue-se de uma análise do volume de controle. Ou seja:

Reagrupando isso, destrichando essas constantes (olhem o capítulo 5, seção 6), temos então:

Agora vamos discutir um pouco sobre essas equações nodais. Como era de esperar, as temperaturas dos nós próximos ao centro do livro atrasam consideravelmente aqueles mais próximos do vidro de exposição. O critério de cura é para . A partir das distribuições de temperatura, note que o nó 10 apenas atinge após minutos e não será curado. Aparece que a região sobre o nó 5 será curada.

(b) O tempo necessário para que o livro chegue a também pode ser visto a partir dos resultados da distribuição de temperatura. As placas mais próximas do prato diminuem até à temperatura de manuseamento seguro com , mas as que estão perto do centro da pilha necessitarão de mais de .

(c) Ao validar códigos de computador é importante que o programa execute um "problema" que tenha uma solução analítica exata. Você deve selecionar o problema de forma que todas as características do código sejam testadas. E isso varia de software para software.