Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 46
Considere a sonda de amostragem de ar do Problema 9-45. Se as linhas de corrente superior e inferior estiverem separadas de na corrente de ar distante, a montante da sonda, faça uma estimativa da velocidade da corrente livre .
Passo 1
E aí, gente, como estão indo? Tudo belezinha? Vamos partir para um problema de função corrente ? Antes de tudo, é necessário dizer que o enunciado da questão está equivocado! A tradução do livro se equivocou e escreveu Problema 9-45 ao invés de mencionar o Problema 9-44. Então nós faremos o exercício de acordo com o Problema 9-44, não de acordo com o Problema 9-45, ok?
O primeiro passo para resolver o problema é entender o que ele pede para a gente calcular e entender quais dados ele nos informa.
A questão quer que a gente calcule a velocidade do ar na sonda de sucção forte (amostragem superisocinética) a partir de dados da função corrente .
A figura abaixo mostra os dados que temos para realizar esse cálculo.
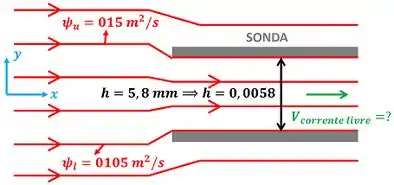
onde é a distância entre as placas que formam a sonda, é a função corrente do fluido que está em contato com a placa de cima e é a função corrente do fluido que está em contato com a placa de baixo. é a coordenada vertical e é a coordenada horizontal que localizam os pontos do escoamento.
Com essas informações, podemos entender como calcular no próximo passo.
Passo 2
Para calcular a componente horizontal da velocidade do ar em função da função corrente , usamos a equação 9-20.
onde é a componente horizontal da velocidade do fluido. Como a componente horizontal vale no nosso caso, podemos reescrever essa fórmula.
Mas como podemos encontrar se não sabemos como varia com e, por isso, não temos como derivar em relação a ?
Passo 3
A resposta para essa pergunta está no próprio enunciado. Ele pede para a gente fazer uma estimativa de . Ele não pede para a gente calcular exatamente quanto vale.
Isso quer dizer que ao invés de calcular exatamente a derivada, nós podemos estimar a derivada. Fazemos isso dividindo a variação total de das duas placas que formam a sonda pela variação total de das duas placas . A equação dessa estimativa se encontra abaixo.
Substituindo os dados na equação acima, achamos uma estimativa para .