Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 67
67 – Considere um tanque de água quente de de diâmetro e de comprimento. O reservatório é colocado sobre o telhado de uma casa; A água dentro do tanque é aquecida a po um coletor solar de placa plana durante o dia. O reservatório é, então, exposto ao ar a com vento a uma velocidade média de durante a noite. Estime a temperatura do reservatório após o período de Suponha que a superfície do tanque esteja na mesma temperatura que a água no interior e que o coeficiente de transferência do calor nas superfícies superior e inferior seja o mesmo das superfícies laterais.
Passo 1
Desenhe o diagrama esquemático do tanque exposto ao ar, como mostrado abaixo:
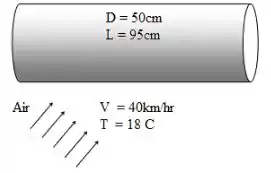
Passo 2
Para na tabela de “Propriedades da água saturada” temos:
Densidade da água,
Calor específico da água,
Obtenha as seguintes propriedades do ar a e (temperatura prevista) na Tabela A-22, “Propriedades do ar à pressão de ” no livro didático.
O número Prandtl é:
Condutividade térmica é:
A viscosidade cinemática é:
Passo 3
Calcule o número de Reynolds:
A velocidade do ar é .
O diâmetro do tanque é .
Como o fluxo é considerado turbulento.
Dessa forma, o número de Nusselt é determinado a partir da seguinte relação:
Passo 4
Podemos achar o coeficiente de transferência de calor por convecção a partir da seguinte relação:
Passo 5
Calcule a quantidade de água (massa de água) no tanque.
Aqui, o comprimento do tanque é e a densidade da água no tanque é
Passo 6
Calcule a transferência de calor da água.
Aqui, o calor específico da água é a , temperatura da água após 45 minutos é e a água aquecida até é .
Passo 7
Calcule a taxa média de transferência de calor.
Passo 8
Calcule a área da superfície do tanque.
Passo 9
Escreva a equação geral da taxa de transferência de calor por convecção.
Temos que:
Logo:
Portanto, a temperatura final do tanque é .
Resposta
Portanto, a temperatura final do tanque é .