Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 132
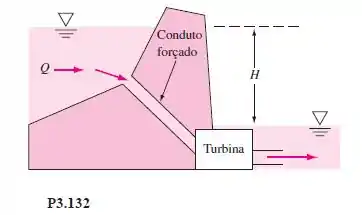
Considere a turbina extraindo energia através de um conduto forçado em uma barragem, como na Figura P3.132. Para escoamento turbulento em dutos (Capítulo 6), a perda de carga por atrito é aproximadamente hp = CQ², em que a constante C depende das dimensões do conduto forçado e das propriedades da água. Mostre que, para uma dada geometria de conduto forçado e vazão variável Q do rio, a máxima potência possível da turbina nesse caso é e ocorre quando a vazão é .
Passo 1
Bora que essa é fácil!!
Vamos primeiro fazer nossas hipóteses como de costume:
- Estado estacionário
- Fluido Incompressivel
Considerando como ponto 1 e 2 a superfície de cima e a superfície de baixo respectivamente, temos a equação de energia dada por:
Note que Daí reduzimos a equação da energia a:
, mas daí:
E a potência da turbina será dada por:
Passo 2
Agora, vamos calcular a máxima potência possível, para isso utilizaremos conceitos de cálculo. Derivaremos função da potência da bomba obtida e igualaremos a equação resultante a zero, para assim obtermos nosso ponto em que a potência será máxima.
E assim, substituindo esta expressão obtida na expressão da potência da turbina obtemos a maior potência possível da turbina, da forma:
Resposta
Conforme demonstrado a potência máxima é e .