Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 42
Como continuação do Problema 9-41, calcule a vazão em volume por unidade de largura para dentro da página da Figura P9-41 com base nos primeiros princípios (integração do campo de velocidade). Compare o seu resultado com aquele obtido diretamente da função corrente. Discuta.
Passo 1
E aí, pessoal, tudo certinho? Esse é um exercício que foi feito para a gente entender melhor a relação entre a função corrente e cálculo de vazão por unidade de largura ( é a largura das placas). Então vamos dominar esse assunto!
O enunciado quer que a gente calcule a vazão por unidade de largura do escoamento do Problema 9-41 de duas formas. A primeira forma é a partir da integração do campo de velocidade como está mostrado na equação abaixo. Por esse caminho, calculamos a vazão volumétrica pela integral e depois dividimos ela pela largura das placas.
A segunda forma é a partir da função de corrente de escoamento incompressíveis (equação 9-25 do livro). Quando subtraímos o valor da função corrente da linha de corrente que está em contato com a placa inferior do valor da função de corrente da linha de corrente que está em contato com a placa superior, encontramos a vazão por unidade de largura que passa pelas placas.
A figura abaixo mostra essas duas formas de se calcular vazão por unidade de largura.
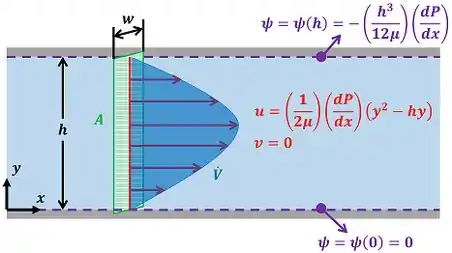
é a componente da velocidade do eixo e é a componente da velocidade no eixo . é a distânica entre as placas. é a função corrente do fluido em contato com a placa superior (onde ). é a função corrente do fluido em contato com a placa de baixo (onde ). é a área transversal pela qual o fluido escoa. é a taxa de variação da pressão ao longo do eixo .
Passo 2
Para integrar a velocidade através da área , temos que considerar e a área do elemento infinitesimal que compõe a área total é igual a largura das placas multiplicada pela espessura .
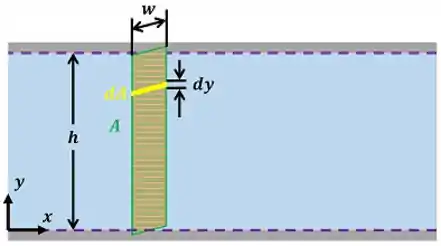
Usando essa informação na integral, achamos:
A velocidade é dada no enunciado do Problema 9-41.
Substituindo essa expressão na integral:
Como e são termos constantes, podemos tirá-los da integral.
Dividindo por :
Passo 3
Agora vamos calcular pelas funções corrente e , usando os valores de e obtidos no Problema 9-41.
Passo 4
Como poderíamos prever, os dois resultados são iguais. Isso acontece porque o escoamento é incompressível. Dessa forma, conseguimos calcular a vazão volumétrica dividida pela largura através da diferença entre dois valores de função corrente . Se o escoamento fosse compressível e permanente, a diferença entre dois valores de função corrente seria igual à vazão mássica de fluido dividida pela largura das placas.