Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 106

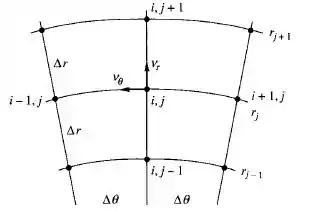
A equação de Laplace em coordenadas polares planas, equação 8.11, é complicada pelo raio variável. Considere a malha de diferenças finitas na figura abaixo, com nós (i,j) igualmente espaçados de Δ θ e Δ r . Deduza um modelo de diferenças finitas para a equação 8.11, semelhante à expressão cartesiana 8.109.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

Foi pedido para modelar

1 r ∂ ∂ r   r ∂ ψ ∂ r + 1 r 2 ∂ 2 ψ ∂ θ 2 = 0

Passo 2

Nesse caso, usando diferenças finitas há duas possibilidades de prosseguirmos, dependendo de onde você queira truncar o primeiro termo. Eu sugiro fazer assim:

1 r i j Δ r r i j + Δ r 2 ψ i , j + 1 - ψ i , j Δ r - r i j - Δ r 2 ψ i , j - ψ i , j - 1 Δ r + ψ i + 1 , j - 2 ψ i j + ψ i - 1 , j     r i j 2 Δ θ 2 ≈ 0

Passo 3

Fazendo um ajuste bonitinho, ficamos com:

2 + 2 ζ ψ i j ≈ ψ i + 1 , j + ψ i - 1 , j + ζ 1 + η ψ i , j + 1 + ζ 1 - η ψ i , j - 1  

Onde ζ = r i j Δ θ Δ r 2 e η = Δ r / 2 r i j

Resposta

2 + 2 ζ ψ i j ≈ ψ i + 1 , j + ψ i - 1 , j + ζ 1 + η ψ i , j + 1 + ζ 1 - η ψ i , j - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja o Problema 4.69. Um engenheiro deseja medir a temperatura superficial do fino revestimento, pintando ele de preto (ε = 0,98) e usando um dispositivo de medição infravermelho para, de forma não in
Um longo cilindro sólido, com diâmetro D = 25 mm, é formado por um núcleo isolante que é coberto por um revestimento metálico altamente polido e muito fino (t = 50 μm), com condutividade térmica de k=
Determine a distribuição de temperaturas em t=30m i n para as condições do Problema 5.116 .(a) Use uma técnica de diferenças finitas explícita, com um incremento de tempo de 600s e um incremento no es
Seja o elemento combustível do Exemplo 5.11 . Inicialmente, o elemento está a uma temperatura uniforme de 250 ° C sem geração de energia. Subitamente, o elemento é inserido no núcleo do reator passand
Considere duas placas, A e B, que estão, cada uma, inicialmente isotérmicas e têm espessura L=5m m . As faces das placas são subitamente colocadas em contato em um processo de união. O material A é ac