Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas Abrangentes - Ex. 2

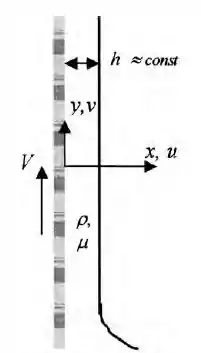
Uma correi move-se para cima com a velocidade V, arrastando um filme de líquido viscoso de espessura h, como mostrado abaixo. Próximo à correia, o filme move-se para cima em virtude da condição de não escorregamento. Em sua borda externa, o filme move-se para baixo por causa da gravidade. Considerando que a única velocidade diferente de zero é v ( x ) , com tensão de cisalhamento nula na borda externa do filme, deduza uma fórmula para (a) v ( x ) , (b) a velocidade média Vméd no filme e (c) a velocidade Vc para a qual não há escoamento líquido para cima nem para baixo. (d) Faça um esboço de v ( x ) para o caso (c).

Passo 1

E aí, gente!! Tudo bem? Vamos que vamos para mais um desafio da mecânica dos fluidos??? Hoje a gente vai lembrar um pouquinho sobre nossa equação de transporte de momentum dado pela equação de Navier-Stokes!!!

(a)

Primeiro vamos as hipóteses que temos:

  1. Escoamento paralelo: u = w = 0   e   v = v x

Isso implicará para gente que a condição da continuidade está sendo satisfeita e além disso implica que as equações para x e z de momento são irrelevantes. Então, ficamos com a equação de Navier Stokes da seguinte forma:

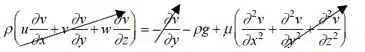
Bem, isso mostra pra gente que o termo convectivo não tem influência na aceleração! Ao final temos que:

ρ g μ = d 2 v d x 2

Vamos integrar isso aí, beleza?

d v d x = ρ g μ x + C 1 → v = ρ g μ x 2 2 + C 1 x + C 2

Passo 2

Vamos utilizar nossas clássicas condições de contorno que dizem que na parede temos tanto velocidade como a tensão de cisalhamento iguais a zero.

τ = μ d v d x x = h = 0

μ ρ g x μ + C 1 ​ x = h = 0 → C 1 = - ρ g h μ

E na parede temos v = V = C 2

Então temos que:

v = V - ρ g h μ x + ρ g 2 μ x 2

Passo 3

(b) A velocidade média é encontrada ao integrarmos a distribuição de velocidade v(x) no filme!!

V m é d i a = 1 h ∫ 0 h v x d x = 1 h V x - ρ g h x 2 2 μ + ρ g x 3 6 μ 0 h = V - ρ g h 2 3 μ

Passo 4

(c) Sabendo-se que h V m é d i a = Q por unidade de profundidade, temos que:

V = ρ g h 2 3 μ

Passo 5

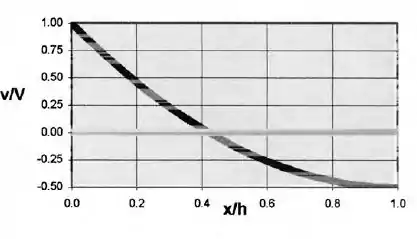
(d) Um gráfico para o caso (c) pode ser feito no excel aí mesmo e olha como ficará!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as nove componentes do tensor de tensão viscosa em coordenadas cilíndricas (veja o Capítulo 9) para o campo de velocidade do Problema 10-95. Discuta.
Explique por que há um excesso de velocidade significativo para os valores intermediários do número de Reynolds nos perfis de velocidade da Figura 10-136, mas não para os valores muito pequenos de R e
A água desce por um tubo vertical apenas por gravidade. O escoamento entre as posições verticais z 1 e z 2 é totalmente desenvolvido e os perfis de velocidade nessas duas posições estão representados
Suponha que o tubo vertical do Problema 10-97 agora é horizontal. Para obter a mesma vazão de volume do Problema 10-106, precisamos fornecer um gradiente de pressão forçado. Calcule a queda de pressão
Para cada afirmativa, decida se ela é verdadeira ou falsa e discuta brevemente a sua resposta.A função potencial de velocidade pode ser definida para escoamentos tridimensionais.A vorticidade deve ser