Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 1

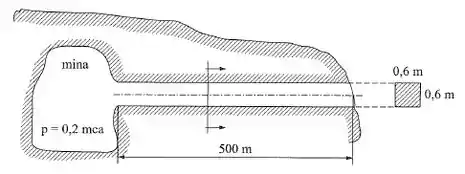
Uma galeria de seção quadrada (0,6 m x 0,6 m) esgota ar de uma mina, onde a pressão é de 0,2 mca, para a atmosfera. Calcular a vazão de ar.

Desprezar as perdas singulares. Sabe-se que ; ; .

Passo 1

Tá legal, vamos começar aplicando o equilíbrio de energia para o sistema entre os pontos 0 (dentro da mina) e 1, na saída da galeria de seção quadrada, assim, temos:

Dentro da mina, podemos assumir , também podemos considerar não haver diferença de cota entre os dois pontos, então , como a saída da galeria está em contato com a atmosfera, temos , então reescrevendo a expressão anterior e abrindo o termo da perda de carga conforme a equação 7.10 dessa seção, temos:

Em que é o fator de atrito, é o comprimento da galeria, é a velocidade do escoamento, que nesse caso é igual a e é o diâmetro hidráulico da seção, então, reescrevendo a expressão e isolando , temos:

Passo 2

Agora vamos calcular os termos da equação anterior, vamos começar pelo diâmetro hidráulico com o auxílio das equações 7.2 e 7.3 dessa seção do livro:

Em que é o raio hidráulico, é a área transversal da seção do escoamento e é o perímetro molhado da área do escoamento. No nosso caso, temos uma seção quadrada, então, da primeira equação, temos:

E, o diâmetro hidráulico será:

Podemos também encontrar a pressão dentro da mina com o dado fornecido no enunciado simplesmente multiplicando esse valor pelo peso específico da água, então, temos:

E, como o enunciado não mencionou nada a respeito de , podemos assumir:

Substituindo esses valores na equação para a velocidade, temos:

Passo 3

Nesse caso, precisamos resolver o problema de maneira iterativa, adotando um arbitrário e depois no final verificando se a hipótese adotada é coerente. Então, precisamos recorrer ao diagrama de Moody (figura 7.16 dessa seção), então, precisamos calcular o valor de que será usado no diagrama, assim, temos:

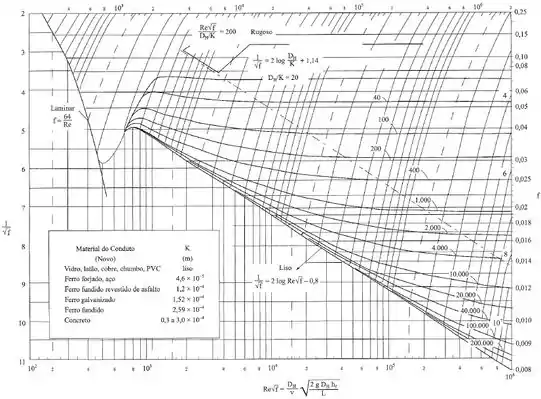
Para resolver o problema, agora precisamos pegar um valor de que está na curva , como na maior parte dos casos teremos altos números de Reynolds, vamos sempre começar com um valor de para o qual a curva no diagrama de Moody seja horizontal (constante), que representa um escoamento rugoso, então, nesse caso:

Então agora vamos retornar à equação para a velocidade do passo 1 e substituir os valores conhecidos:

Agora devemos verificar se o valor de velocidade encontrado é coerente com o que assumimos para encontrar , então, calculando o Reynolds para esse caso:

Olhando para o diagrama de Moody, para esse valor de , a curva com pode ser considerada constante, então assumimos corretamente o valor de e o valor de que encontramos é válido.