Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 30
As grandes turbinas eólicas disponíveis comercialmente incluem diâmetros de até e geram mais de de energia elétrica em condições ótimas de projeto. Considere uma turbina eólica com envergadura de lâmina de sujeita a ventos constantes de . Se a eficiência combinada de turbina e gerador da turbina eólica for de , determine (a) a potência gerada pela turbina e (b) a força horizontal exercida pelo vento sobre o mastro de suporte da turbina. Tome a densidade do ar como e despreze os efeitos do atrito.
Passo 1
O enunciado quer primeiro que a gente calcule a potência gerada pela combinação entre turbina eólica. Depois, a questão pede para a gente calcular a força horizontal que o vento exerce sobre o mastro da turbina.
O primeiro passo para esses dois cálculos é escolher o volume de controle que vamos usar para estudar a turbina. Como queremos informações sobre a turbina, vamos imaginar que o volume de controle é a região do espaço que engloba a turbina e seu mastro. A figura abaixo mostra essa situação.
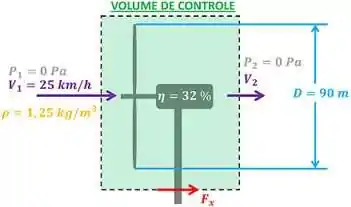
é a velocidade do ar entrando no volume de controle e é a velocidade do ar saindo do volume de controle. e são as pressões manométricas do ar entrando e do ar saindo do volume de controle respectivamente. Essas duas pressões manométricas valem zero por que o ar que entra e sai do volume de controle tem a mesma pressão que a atmosfera.
é a densidade do ar. Como o enunciado só dá um valor pra densidade do ar, podemos considerar o escoamento incompressível (). é a envergadura das lâminas da turbina é a força horizontal que o vento faz no mastro. é a eficiência combinada da turbina com o gerador.
No próximo passo vamos aprender a calcular atrave´s de uma fórmula.
Passo 2
A eficiência da turbian e do gerador é calculada dividindo a potência real que eles geram pela potência máxima que esses dois equipamentos podem produzir juntos. Sabendo disso, podemos criar uma fórmula para .
A máxima potência é gerada, quando a turbina e o gerador conseguem transformar toda energia mecânica do vento em energia elétrica. Ou seja, a máxima potência é alcançada, quando esses equipamentos extraem toda a energia mecânica do ar em movimento. A energia mecânica do vento que entra no volume de controle a cada segundo é a igual à sua energia cinética.
onde é a vazão mássica de ar que passa pela turbina. Ela é igual a:
é a área por onde o vento passa e colide com a turbina. Como as lâminas da turbina t~em apenas um movimento circular, a área que através da qual o vento passa e colide com a turbina é a área de um círculo. A imagem abaixo explica isso.
Substituindo a fórmula da vazão na fórmula da energia mecânica do vento, encontramos?
Como é igual a , temos que:
Substituindo essa fórmula na equação da potência real gerada , achamos:
Passo 3
Substituindo esses dados na fórmula que criamos, achamos o valor de . Antes disso, temos que lembrar de converter a velocidade de para , dividindo ela por .
Passo 4
Para encontrar a força precisamos aplicar a segunda lei de Newton (equação da quantidade de movimento) ao volume de controle. Podemos considerar que o escoamento de ar ocorre em regime permanente, porque as turbina geralmente operam dessa forma. Como estamos interessados apenas na força do eixo , vamos usar a equação do livro (segunda lei de Newton no eixo para volumes de controle em regime permanente).
onde é o somatório das forças horizontais (no eixo ) sobre o volume de controle, é o fator de correção para o escoamento que entra no volume de controle. é o fator de correção para o escoamento que sai do volume de controle. Esses dois fatores de conversão valem , porque esse é o valor do fator de correção para escoamentos livres na atmosfera.
é a velocidade do ar no eixo entrando no cotovelo. é a velocidade do ar no eixo saindo do cotovelo. Ela é igual à velocidade , porque é uma velocidade horizontal.
pode ser calculada através da conservação de energia do volume de controle. Como nenhuma energia é perdida por atrito (o enunciado afirma isso), a energia cinética do ar que entra no volume de controle se transforma apenas em potência e em energia cinética do ar que sai do volume de controle. Logo:
Além disso, a velocidade é horizontal. Logo, sua componente horizontal é igual à .
Substituindo essas informações na fórmula de , encontramos:
A única força do eixo é a força . A força que a pressão atmosférica exerce sobre o volume de controle não é contabilizada, porque é atua sobre todo o volume de controle e seu efeito acaba sendo cancelado.
Substituindo isso na equação anterior de , encontramos:
Passo 5
Finalmente podemos substituir os dados na fórmula de para encontrar seu valor.