Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 96

Um sistema de frenagem de emergência de um avião militar consiste em um grande paraquedas de 6 m de diâmetro. Se o avião tem massa de 8500 kg e aterrissa a 400 km/h, determine o tempo e a distância para os quais o avião é desacelerado para 100 km/h somente pelo paraquedas. Trace o gráfico da velocidade em função da distância e também em função do tempo. Qual é a máxima “força g” experimentada? Um engenheiro propõe que menos espaço seria tomado, substituindo o grande paraquedas por três paraquedas não interferentes, cada um com diâmetro de 3,75 m. Que efeito isso teria sobre o tempo e a distância de desaceleração do avião para 100 km/h?

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que as respectivas áreas do paraquedas e de 3 paraquedas são:

A 1 = π 4 D 1 2

A 3 = π 4 D 3 2

Substituindo os dados:

A 1 = 28,274 m 2

A 3 = 11,045 m 2

Aplicando a segunda lei de Newton para a aeronave:

M d V d t = - C A 1 2 ρ A V i 2

Integrando os dois lados:

V t = V i 1 + C A ρ A 2 M V i t → e q   1

Integrando de novo em relação a variável t :

x t = 2 M C A ρ A ln ⁡ 1 + C A ρ A 2 M V i t → e q   2

Combinando as equações 1 e 2 e eliminando o t :

x = 2 M C A ρ A ln ⁡ V i V → e q   3

A máxima força g é dada por:

d V d t g = - C A ρ A V 2 2 M g

Já para 3 paraquedas, basta substituir A = 3 A :

V t = V i 1 + 3 C A ρ A 2 M V i t

x t = 2 M 3 C A ρ A ln ⁡ 1 + 3 C A ρ A 2 M V i t

Agora, com a ajuda do Excel, podemos determinar o valor da máxima força g:

g m á x = - 3 , 66

Passo 2

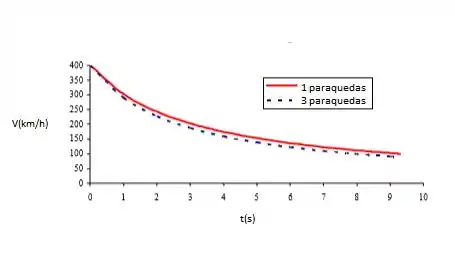
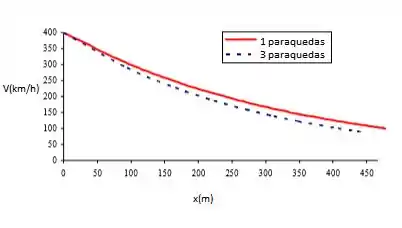
Agora, basta fazer os gráficos no Excel:

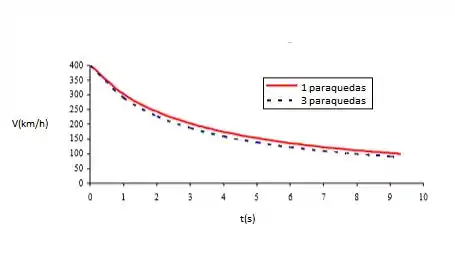
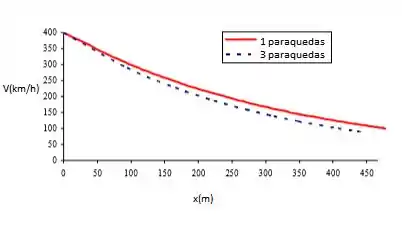
Resposta

g m á x = - 3,66

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar escoa a M a ∞ = 3,0 ao redor de um aerofólio em formato de losango duplamente simétrico cujos ângulos inclusos dianteiro e traseiro são ambos de 24º. Para ângulo de ataque nulo, calcule o coeficien
Um avião de transporte supersônico tem uma massa de 65 Mg e voa a 11 km de altitude padrão a um número de Mach de 2,25. Se o ângulo de ataque é de 2º e suas asas podem ser aproximadas por placas plana
Um aerofólio supersônico tem um formato simétrico parabólico para as superfícies superior e inferior y u , l = ± 2 t x C - x 2 C 2 tal que a espessura máxima é t em x = 1 2 C . Calcule o coeficiente d
Um aerofólio fino em formato de arco de círculo é mostrado na Figura P9.156. O bordo de ataque é paralelo à corrente livre. Utilizando a teoria linearizada do escoamento supersônico (pequenos ângulos
O avião F-35 na Figura 9.30 tem uma envergadura de asa de 10 m e uma área de asa de 41,8 m². Ele voa a cerca de 10 km de altitude com um peso total em torno de 200 kN. A essa altitude, o motor desenvo