Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 107

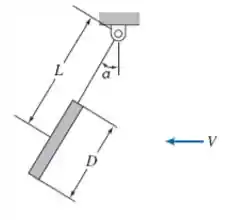
Um disco circular é pendurado em uma corrente de ar a partir de um suporte articulado, conforme mostrado. Em um experimento de túnel de vento, realizado no ar a 15 m/s com um disco de 25 mm de diâmetro, ∞ foi medido como 10°. Para estas condições, determine a massa do disco. Considere que o coeficiente de arrasto para o disco aplica­se quando a componente da velocidade do vento normal ao disco é usada. Considere também que o arrasto na haste e o atrito no pivô são desprezíveis. Trace uma curva teórica de ≚ como uma função da velocidade do ar.

Passo 1

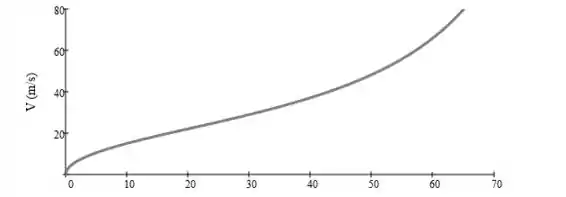
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede para encontramos a massa do disco e para traçarmos um gráfico α × V . Sabendo disso, temos:

C D = F D 1 2 ρ V 2 A ∑ M = 0

Somando os momentos:

W L sin ⁡ α - F n L = 0 F n = 1 2 ρ V n 2 A C D

Substituindo:

M g sin ⁡ α = 1 2 ρ V cos ⁡ α 2 π D 2 4 C D Temos que:

ρ = 1.225 k g m 3 V = 15 m s D = 25   m m α = 10 ° C D = 1,17

M = 0,0451   k g

Agora, podemos substituir em:

V = 8 M g π ρ D 2 C D ∙ tan ⁡ α cos ⁡ α V = 35,5 m s tan ⁡ α cos ⁡ α

Passo 2

Com esses dados, podemos construir nosso gráfico. Ele fica assim:

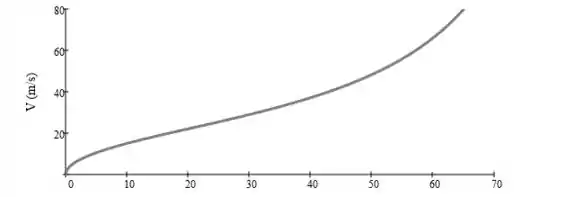
Resposta

M = 0,0451   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A teoria do aerofólio de Ackeret da Equação (9.104) é concebida para velocidades supersônicas moderadas, 1,2 C S e (b) C A para um aerofólio em placa plana a α =5 º º e M a ∞ = 8,0 usando a teoria de
Uma nova pizzaria está para ser inaugurada. Naturalmente, eles vão oferecer serviço gratuito de entrega e, portanto, precisam de um pequeno carro de entrega com um grande letreiro de anúncio fixado. O
Ar a 20°C e 1 atm escoa a Vméd = 5 m/s entre placas paralelas lisas e longas de um trocador de calor, separadas de 10 cm, como na Figura PA7.2. Propõe-se adicionar um número muito grande de placas int
Os dados bidimensionais de sustentação e arrasto para o aerofólio Naca 2412 com 2% de arqueamento (da Referência 12) podem ser ajustados com precisão pelas seguintes fórmulas: C S = 0,178 + 0,109 α -
Um barco fluvial com 400 kg de massa é suportado por um hidrofólio retangular com razão de aspecto 8, 2% de arqueamento e 12% de espessura. Se o barco navega a 7 m/s e a 5 2,5o, avalie (a) o comprimen