Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 98

Deseja-se usar um balão de ar quente com um volume de 9060   m 3 para passeios planejados em manhãs de verão quando a temperatura do ar é de 9 ° C . A tocha aquecerá o ar dentro do balão a uma temperatura de 70 ° C . Ambas as pressões, dentro e fora do balão, serão padrão ( 101,3   k P a ) . Que massa o balão pode levar (cesto, combustível, passageiros, itens pessoais e os próprios equipamentos do balão) para que um empuxo equilibrante seja garantido? E que massa pode ser levada para o balão subir com uma aceleração vertical de 0,75 m s 2 ? Para isso, considere que tanto o balão quanto o ar interno tenham que ser acelerados, bem como

algum ar vizinho (que passa pelo balão). A regra prática é que a massa total sujeita à aceleração é igual à massa do balão, com todos seus pertences, e duas vezes a massa do seu volume de ar. Dado que o volume de ar quente é fixo durante o voo, o que os balonistas

podem fazer quando eles querem descer?

Passo 1

Nesse problema, temos um balão de ar quente e o objetivo é encontrar a massa máxima de balão para flutuabilidade neutra; massa para aceleração inicial de 0,75 m s 2 . Para isso, supomos que o ar é estático e incompressível, e um gás ideal. Utilizaremos as equações a seguir:

F e m p u x o = ρ g V , força de empuxo

∑ F y = 0 , somatório de forças no sentido de y

Passo 2

Pelo diagrama podemos fazer a seguinte analise de forças:

F B - W a r   q u e n t e   - W c a r g a = 0

ρ a t m g V - ρ a r   q u e n t e g V - M g = 0

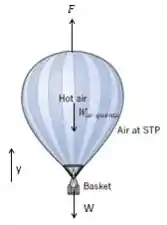
Isolamos a massa e fazemos os devidos calculos:

M = V ρ a t m - ρ a r   q u e n t e = V p a t m R 1 T a t m - 1 T a r   q u e n t e

M = 9060   m 3 × 101,3 ×   10 3 P a 287,058 J k g · K 1 282 - 1 343 = 2016,3   k g

Para a aceleração inicial, fazemos

F = F B - W a r   q u e n t e   - W c a r g a = 0

F = ρ a t m - ρ a r   q u e n t e g V - M n o v o g = M a = M n o v o + 2 ρ a r   q u e n t e   V a

Isolando para encontramos a outra massa, temos:

M n o v o = V ρ a t m - ρ a r   q u e n t e g - 2 ρ a r   q u e n t e   a a + g = V p a t m a + g g 1 T a t m - 1 T a r   q u e n t e - 2 a T a r  

Logo,

M n o v o = V p a t m a + g g 1 T a t m - 1 T a r   q u e n t e - 2 a T a r   q u e n t e

M = 9060   m 3 × 101,3 ×   10 3 P a 0,75 m s 2 + 9,81 m s 2 9,81 m s 2 1 282 - 1 343 - 2 × 0,75 m s 2 343 = 158 × 10 3 k g

Portanto, para fazer o balão subir ou descer durante o vôo, o ar precisa ser aquecido a uma temperatura mais alta ou deixar esfriar.

Resposta

o ar precisa ser aquecido a uma temperatura mais alta ou deixar esfriar.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um balão esférico com hélio tem 2,5 m de diâmetro e uma massa total de 6,7 kg. Quando ele é solto na atmosfera padrão dos Estados Unidos, a que altitude ele irá estabilizar-se?
Uma bola sólida de alumínio (d = 2,7) com 7 cm de diâmetro e uma bola sólida de latão (d = 8,5) se equilibram perfeitamente quando submersas em um líquido, como mostra a Figura P2.108. (a) Se o fluido
Um densímetro flutua em um nível que é uma medida da densidade do líquido. A haste é de diâmetro constante D e o peso no fundo estabiliza o corpo para flutuar verticalmente, como mostra a Figura P2.10
Um balão de ar quente deve ser projetado para suportar o cesto, as cordas e uma pessoa, totalizando um peso de 1.300 N. O material do balão tem uma massa de 60 g/m2. O ar ambiente está a 25°C e 1 atm.
Uma boia de mastro é uma haste flutuante com peso ajustado para flutuar e sair verticalmente para fora, como mostra a Figura P2.113. Ela pode ser usada para medidas ou marcações. Considere que a boia