Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 17

Deslocamento de inteiros à direita. Escreva um

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

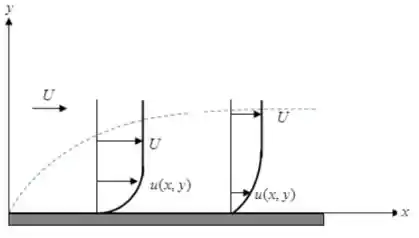
O diagrama mostra a aproximação para duas lâminas dimensionais incompressíveis e a camada limite na superfície

Passo 2

A equação de continuidade em forma bidimensional é,

[[,(del u)/(del x),+,(del v)/(del y),=,0],[,(del v)/(del y),=,-,(del u)/(del x),.,.,.,(,1,)]]

Temos a equação,

u = U (2 (y)/(delta) - 2 (y^3)/(delta^3) + (y^4)/(delta^4)) Agora, substituir u na equação (1)

[[(del v)/(del y),,=,-,(del)/(del x),U,(2 (y)/(delta) - 2 (y^3)/(delta^3) + (y^4)/(delta^4))],[,,=,-,U,[- (2 y)/(delta^2) (d delta)/(d x) + (6 y^3)/(delta^4) (d delta)/(d x) - (4 y^4)/(delta^5) (d delta)/(d x)]],[,,=,-,U,(d delta)/(d x),[- (2 y)/(delta^2) + (6 y^3)/(delta^4) - (4 y^4)/(delta^5)]],[d,v,,=,-,U,(d delta)/(d x),[- (2 y)/(delta^2) + (6 y^3)/(delta^4) - (4 y^4)/(delta^5)],d,y]]

Passo 3

Integrando em ambos os lados,

[[int,d,v,,=,int_0^y,,-,U,(d delta)/(d x),[- (2 y)/(delta^2) + (6 y^3)/(delta^4) - (4 y^4)/(delta^5)],d,y],[v,,=,2,U,(d delta)/(d x),[|(y^2)/(2 delta^2)|_0^y - |(3 y^4)/(4 delta^4)|_0^y + |(2 y^5)/(5 delta^5)|_0^y]],[,,=,2,U,(d delta)/(d x),[(y^2)/(2 delta^2) - (3 y^4)/(4 delta^4) + (2 y^5)/(5 delta^5)]]]

Portanto, a expressão do componente de velocidade v ( x , y ) é 2 U (d delta)/(d x) [(y^2)/(2 delta^2) - (3 y^4)/(4 delta^4) + (2 y^5)/(5 delta^5)]

Passo 4

b) Substitua: 1 m para x , 3 m // s para U , 0.011 m para delta Onde, temos

delta = C x^(1 // 2)

A partir da equação acima

[[C,,=,(delta)/(x^(1 // 2))],[,,=,(0.011)/(1^(1 // 2))],[,,=,0.011]]

Passo 5

Diferenciar delta em relação a x ,

[[(d delta)/(d x),,=,C,(d x^(1 // 2))/(d x)],[,,=,(C)/(2),x^(- 1 // 2)],[,,=,(delta)/(2 x^(1 // 2)),x^(- 1 // 2)],[,,=,(delta)/(2 x)]]

O componente de velocidade é v máximo na borda externa da camada limite quando, y = delta portanto, o componente de velocidade máxima é dado por,

[[,v,=,(3 delta)/(x),[(y^2)/(2 delta^2) - (3 y^4)/(4 delta^4) + (2 y^5)/(5 delta^5)]],[,,=,(3 xx 0.011)/(1),[(1)/(2) - (3)/(4) + (2)/(5)]],[,,=,0.00495,,m,//,s]]

Portanto, o componente de velocidade máxima v é 0.00495 m // s

Resposta

a) v = 2 U (d delta)/(d x) [(y^2)/(2 delta^2) - (3 y^4)/(4 delta^4) + (2 y^5)/(5 delta^5)]

b) v = 0.00495 m // s

Exercícios de Livros Relacionados

Um campo de escoamento incompressível tem os componentes cilíndricos v θ = C r , v z = K R 2 - r 2 , v r = 0 , em que C e K são constantes e r ≤ R , z ≤ L . Esse escoamento satisfaz a continuidade? O
Para o escoamento incompressível em coordenadas polares, qual é a forma mais geral de um movimento puramente circulatório, v θ = v θ ( r ,θ ,t ) e v r = 0 , que satisfaz a continuidade?
Qual é a forma mais geral de um padrão de escoamento incompressível puramente radial em coordenadas polares, v r = v r ( r ,θ ,t ) e v θ = 0 , que satisfaz a continuidade?
Considere a distribuição de velocidade em coordenadas polares planas v r = C r v θ = K rv z = 0 em que C e K são constantes. (a) Determine se a equação da continuidade é satisfeita. (b) Fazendo o esbo
Um pistão comprime gás em um cilindro movendo-se a uma velocidade constante V , como na Figura P 4.18 .Admita que a massa específica do gás e a posição do pistão em t = 0 sejam ρ 0 e L 0 , respectivam