Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 19
Processos em batelada são frequentemente usados em operações químicas e farmacêuticas para obter uma composição química desejada no produto final e tipicamente envolvem uma operação de aquecimento transiente para levar os reagentes da temperatura ambiente para a temperatura necessária no processo. Seja uma situação na qual uma substância química de massa específica e calor específico ocupa um volume de em um vaso isolado termicamente. A substância deve ser aquecida da temperatura ambiente, , até uma temperatura de processo igual a , pela passagem de vapor d’água saturado a através da serpentina no interior do vaso, cujo tubo tem parede delgada e de diâmetro. O vapor condensando no interior da serpentina mantém um coeficiente convectivo no seu interior de , enquanto o líquido altamente agitado no interior do vaso mantém um coeficiente convectivo externo de .
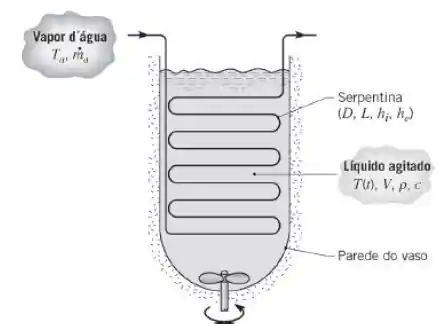
Se a substância deve ser aquecida de , em minutos, qual é o comprimento necessário da serpentina submersa?
Passo 1
Vamos lá! Nosso problema nos pede o comprimento da serpentina para o aquecimento desejado, mas antes que tal desenharmos um esboço do comportamento desse problema pra entendermos o que o ocorre. Fica assim.
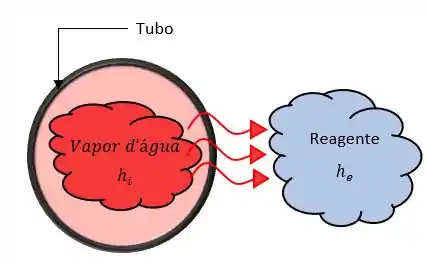
Agora vamos as nossas famosas considerações pra resolver nosso problema.
Passo 2
Podemos considerar nossa questão como um aquecimento de regime transiente, de capacitância global, onde o aquecimento devido ao vapor é balanceado pelo aumento da temperatura na reação química, assim nosso balanço de energia fica:
Rearranjando e integrando os dois lados temos:
Sendo
Assim nossa equação para fica:
Lembrando que
Isso é tudo pessoal! Essa questão não é complicada, só precisamos estar atentos as considerações pra simplificar o máximo possível o balanço de energia!