Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 43

Seja a transferência de calor unidimensional (radial) em um sistema de coordenadas cilíndricas em regime estacionário com geração volumétrica de calor.

(a) Deduza a equação de diferenças finitas para qualquer nó interior m.

(b) Deduza a equação de diferenças finitas para o nó n localizado no contorno externo sujeito a um processo de convecção ( T ∞ , h ) .

Passo 1

Temos que encontrar a equação de diferenças finitas para um ponto nodal em um sistema de coordenadas cilíndricas. Para isso, nosso primeiro passo é definir o volume de controle:

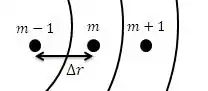
As taxas de transferência de calor envolvidas são:

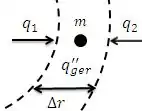
Nosso próximo passo é realizar o balanço de energia para o sistema em regime estacionário:

d E d t = E ˙ e n t - E ˙ s a í d a + E ˙ g e r

0 = E ˙ e n t + E ˙ g e r

0 = q 1 + q 2 + q g e r ' ' × V o l u m e

Passo 2

Vamos agora descrever cada taxa de transferência de calor separadamente:

q 1 = q m - 1 → ( m )

q 1 = k A L ∆ T

q 1 = k 2 π R m - ∆ r 2 ∙ l ∆ r T m - 1 - T m

q 2 = q m + 1 → ( m )

q 2 = k A L ∆ T

q 2 = k 2 π R m + ∆ r 2 ∙ l ∆ r T m + 1 - T m

q 3 = q g e r ' ' × V o l u m e

q 3 = q g e r ' ' 2 π R m ∆ r l

Voltando para o balanço de energia:

k 2 π R m - ∆ r 2 ∙ l ∆ r T m - 1 - T m + k 2 π R m + ∆ r 2 ∙ l ∆ r T m + 1 - T m + q g e r ' ' 2 π R m ∆ r l = 0

Considerando que a cada espaço ∆ r há um novo ponto nodal podemos escrever R m = m ∆ r :

k 2 π m ∆ r - ∆ r 2 ∙ l ∆ r T m - 1 - T m + k 2 π m ∆ r + ∆ r 2 ∙ l ∆ r T m + 1 - T m + q g e r ' ' 2 π m ∆ r ∆ r l = 0

m - 1 2 T m - 1 - T m + m + 1 2 T m + 1 - T m + q g e r ' ' m ∆ r 2 k = 0

m - 1 2 T m - 1 + m + 1 2 T m + 1 - 2 m T m + q g e r ' ' m ∆ r 2 k = 0

Passo 3

O item (b) nos pede agora para considerar que o ponto nodal está localizado no contorno externo do cilindro e está sujeito a um processo de convecção. Ou seja, iremos agora repetir o mesmo procedimento, considerando q 2 = q c o n v . Vamos lá?

O balanço de energia para esta situação será:

0 = q 1 + q 2 + q g e r ' ' × V o l u m e

Descrevendo cada taxa separadamente:

q 1 = q n - 1 → ( n )

q 1 = k A L ∆ T

q 1 = k 2 π R n - ∆ r 2 ∙ l ∆ r T n - 1 - T n

q 2 = q c o n v

q 2 = h A ∆ T

q 2 = h ( 2 π R n l ) T ∞ - T n

q 3 = q g e r ' ' × V o l u m e

q 3 = q g e r ' ' 2 π R n ∆ r 2 l

Substituindo no balanço de energia:

k 2 π R n - ∆ r 2 ∙ l ∆ r T n - 1 - T n + h 2 π R n l T ∞ - T n + q g e r ' ' 2 π R n ∆ r 2 l = 0

Aplicando R n = n ∆ r :

k 2 π n ∆ r - ∆ r 2 ∙ l ∆ r T n - 1 - T n + h 2 π n ∆ r l T ∞ - T n + q g e r ' ' 2 π n ∆ r ∆ r 2 l = 0

n - 1 2 T n - 1 - T n + h n ∆ r k T ∞ - T n + q g e r ' ' n ∆ r 2 2 k = 0

n - 1 2 T n - 1 + h n ∆ r k T ∞ - n - 1 2 + h n ∆ r k T m + q g e r ' ' n ∆ r 2 2 k = 0

Resposta

(a) m - 1 2 T m - 1 + m + 1 2 T m + 1 - 2 m T m + q g e r ' ' m ∆ r 2 k = 0 .

(b) n - 1 2 T n - 1 + h n ∆ r k T ∞ - n - 1 2 + h n ∆ r k T m + q g e r ' ' n ∆ r 2 2 k = 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja a configuração nodal 4 da tabela 4.2 . Deduza as equações de diferenças finitas, para condições de regime estacionário, nas seguintes situações.(a) O contorno superior do vértice externo está per
Um dos pontos fortes dos métodos numéricos é a sua capacidade de lidar com condições de contorno complexas. No esboço, a condição de contorno muda de fluxo térmico especificado, q s ' ' (para dentro d
As superfícies superior e inferior de uma barra de condução são resfriadas por convecção com ar a T ∞ , com h s ≠ h i . As laterais são resfriadas pela manutenção de contato com sumidouro de calor a T
Seja a malha bidimensional ( ∆ x = ∆ y ) representando condições de regime estacionário, sem geração volumétrica interna de calor, em um sistema com condutividade térmica k . Um dos contornos é mantid
Determine as expressões para q ( m - 1 , n ) → ( m , n ) ,q m + 1 , n → ( m , n ) ,q m ,n + 1 → ( m , n ) e q m ,n - 1 → ( m , n ) , na condução associada a um volume de controle que abrange dois dife