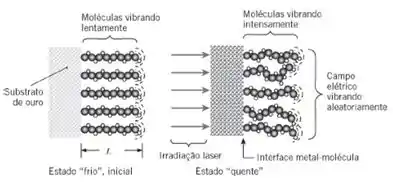
Eletrônica molecular é um campo emergente associado á computação e armazenamento de dados utilizando transferência de energia em escala molecular. Nessa escala, energia térmica está associada exclusivamente à vibração de cadeias moleculares. A principal resistência à transferência de energia nestes dispositivos propostos é a resistência de contato na interface metal-molécula. Para medir a resistência de contato, moléculas individuais são autoarranjadas em um padrão regular sobre um substrato de ouro muito fino. O substrato é subitamente aquecido por um pequeno pulso de irradiação laser, simultaneamente transferindo energia térmica para as moléculas. As moléculas vibram intensamente em seu estado “quente” e a sua intensidade vibracional pode ser medida pela detecção da aleatoriedade do campo elétrico produzido pelas extremidades das moléculas, como indicado pelas linhas circulares tracejadas no esquema.

Moléculas com massa específica e calor específico têm um comprimento inicial em repouso de . A intensidade da vibração molecular aumenta exponencialmente de um valor inicial até um valor no regime estacionário , com a constante de tempo associada à resposta exponencial igual a . Supondo que a intensidade da vibração molecular representa a temperatura na escala molecular e que cada molécula pode ser vista como um cilindro com comprimento inicial e seção transversal , determine a resistência térmica de contato, , na interface metal-molécula.

Passo 1

Passo 2

Resposta