Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 24

Em um experimento de processamento de material realizado a bordo do ônibus espacial, uma esfera de nióbio, com um revestimento com 10   m m de diâmetro, é removida de um forno a 900 ° C e resfriada até uma temperatura de 300 ° C . Embora haja variação das propriedades do nióbio neste intervalo de temperaturas, valores constantes podem ser supostos com uma aproximação aceitável, sendo ρ   =   8600   k g / m 3 , c   =   290   J / ( k g   ·   K ) e k   =   63   W / ( m   ·   K ) .

(a)Se o resfriamento for conduzido em uma grande câmara, na qual há vácuo e cujas paredes estejam a 25 ° C , determine o tempo requerido para atingir a temperatura final, se o revestimento estiver polido e tiver uma emissividade ε   =   0,1 . Quanto tempo demoraria se o revestimento estivesse oxidado com ε   =   0,6 ?

(b)Para reduzir o tempo requerido para o resfriamento, considera-se a imersão da esfera em uma corrente de um gás inerte na qual T ∞ = 25 ° C e h = 200   W / ( m 2 · K ) . Desprezando a radiação, qual é o tempo requerido para o resfriamento?

(c)Considerando os efeitos da radiação e da convecção, qual é o tempo requerido para o resfriamento, se h   =   200   W / ( m 2   ·   K ) e ε   =   0,6 ? Explore o efeito no tempo de resfriamento de se variar independentemente h e ε .

Passo 1

Beleza pessoas, vamos assumir que a temperatura é uniforme em todo o tempo, isso vai facilitar o entendimento dos métodos aplicados. (a) Se o resfriamento é exclusivamente por radiação, o tempo necessário é determinado a partir de Eq. (5.18). Portanto, sem enrolação:

t = 8600 k g m 3 290 J k g ⋅ K 0.01 m 24 0.1 5.67 × 10 - 8 W m 2 ⋅ K 4 298 K 3 ln ⁡ | 298 + 573 298 - 573 | - ln ⁡ 298 + 1173 298 - 1173  

Logo,

t = 1190   s

Isso para a emissividade = 0.1 . Para emissividade = 0.6 , esse negocio esfria 6 vezes mais rápido, logo:

t = 199   s

Passo 2

(b) Se o resfriamento for exclusivamente por convecção, Eq. (5,5), temos:

t = ρ c D 6 h ln ⁡ T i - T ∞ T f - T ∞ = 8600 k g m 3 290 J k g ⋅ K 0.01 m 1200 W m 2 ⋅ K ln ⁡ 875 275

Logo,

t = 24.1 s

Passo 3

(c) Tanto com radiação quanto com convecção, o histórico de temperatura pode ser obtido na Eq. (5,15).

ρ π D 3 6 c d T d t = - π D 2 h T - T ∞ + ε σ ( T 4 - T s u r 4

Integrando numericamente, de T i = 1173 K em t = 0 para T = 573 K , obtemos:

t = 21   s

Os tempos de resfriamento correspondentes a mudanças representativas em e h são tabulados da seguinte forma:

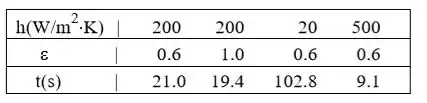
Para valores de h representativos de convecção forçada, a influência da radiação é secundária, mesmo para uma emissividade máxima possível de 1,0. Portanto, para acelerar o resfriamento, é necessário aumentar h. Entretanto, se o resfriamento for por convecção natural, a radiação é significativa.

Resposta

a ) t = 1190 s   ε = 0.1 ,     t = 199 s   ε = 0.6

b ) t = 24.1 s

c )   t = 21 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Válvulas de motor (k = 48 W/m.K, c p = 440 J/kg.K ρ = 7840 kg/m³) são aquecidos a 800 °C na seção de tratamento térmico de uma fábrica de válvulas. As válvulas são imersas em banho de óleo a uma tempe
Válvulas de motor (k = 48 W/m.K, c p = 440 J/kg.K ρ = 7840 kg/m³) são aquecidos a 800 °C na seção de tratamento térmico de uma fábrica de válvulas. As válvulas são imersas em banho de óleo a uma tempe
Um rolo longo de chapa de aço de manganês de 2 m de largura e 0,5 cm de espessura deixa o forno a 820 °C e deve ser imerso no banho de óleo ( c P = 2,0k J k g . K ) . A chapa metálica se desloca a uma
Repita o Prob. 4-132 para o fio de cobre ((ρ = 8950 kg/m³, c P = 0,383k J k g . K , k=386W / m . Keα=1,13 x 10 - 4m ² / s ² ) .
Grandes chapas de aço com 1,0 cm de espessura são resfriadas de 600°C a 100°C por imersão em um reservatório de óleo mantido a 30°C. O coeficiente médio de transferência de calor para as duas faces da