Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 35

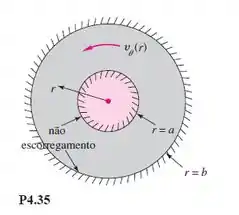
Das equações de Navier-Stokes para escoamento incompressível em coordenadas polares (Apêndice D para coordenadas cilíndricas), encontre o caso mais geral de movimento puramente circulatório v θ r ,   v r = v z = 0 , para escoamento sem escorregamento entre dois cilindros concêntricos fixos, como na Figura P4.35.

Passo 1

Eitaaaa, bora pra mais uma!

Aqui temos um procedimento idêntico à questão 4.32, iremos substituir nosso v θ ( r ) , v r = v z = 0 , dentro da equação de Navier-Stokes, da uma olhadela lá na questão 4.32 que é idêntico.

Chegaremos numa EDO da seguinte forma:

f ' ' + 1 r   f ' - 1 r 2 f = 0

Tendo duas possíveis resoluções, são elas:

f 1 = C 1 r           e               f 2 = C 2 r

Sendo uma solução geral dada por:

v θ = C 1 r + C 2 r

Substituindo os raios a e b, de forma onde não temos escorregamento, teremos:

v θ a = 0 = C 1 a + C 2 a

v θ b = 0 = C 1 b + C 2 b

Para isso ser verdades, precisaremos de C 1 = C 2 = 0 ou então que v θ = 0 .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar a 20°C flui com velocidade V = 80,0 m/s sobre uma placa plana lisa de comprimento L = 17,5 m. Faça um gráfico do perfil da camada limite turbulenta em variáveis físicas (u em função de y) na distân
Escreva a equação de Bernoulli e discuta como ela difere entre uma região de escoamento sem viscosidade, rotacional e uma região de escoamento viscoso irrotacional. Qual dos casos é mais restritivo (c
Que propriedades do escoamento determinam se uma região do escoamento é rotacional ou irrotacional? Discuta.
Escreva as componentes da equação de Euler desenvolvendo-se tanto quanto possível em coordenadas (r, θ, z) e (ur, uθ, uz). Suponha que a gravidade age em alguma direção arbitrária.
Usando os resultados do Problema 10-38, calcule a constante de Bernoulli como uma função da coordenada radial r.