Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 40
Usando os resultados do Problema 10-38, calcule a constante de Bernoulli como uma função da coordenada radial r.
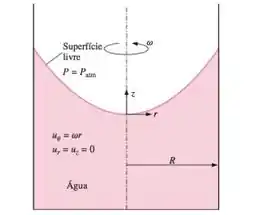
Passo 1
Na questão mencionada aí, a gente viu que o campo de pressão é dado por:
Passo 2
A equação de Bernoulli para o estado estacionário, fluido incompressível e regiões invíscidas é:
No exercício 10-38 e também na imagem, você verá que o campo de velocidade é dito como tendo ur = uz = 0 e uθ = wr, V2 = w²r² e com isso, olha o que a gente pode fazer na equação de Bernoulli!!
Passo 3
Agora olha o que podemos fazer: Se a gente tem o campo de velocidade dado pelo passo 1, basta substituirmos na equação de Bernoulli e encontrarmos a constante.
Resposta
Exercícios de Livros Relacionados
5.51 Após uma chuva, a concentração de sedimentos em um certo ponto de um rio aumenta à taxa de 100 partes por milhão (ppm) por hora. Além disso, a centração de sedimentos aumenta com a distância rio
A componente x da velocidade em um campo de escoamento bidimensional e incompressível é dada por u = A x 2 ; A = 3,28m - 1 . s - 1 e as coordenadas são medidas em metros, Não há componente ou variação
A componente x da velocidade em um campo de escoamento bidimensional, incompressível, é dada por u = A x y , as coordenadas são medidas em metros e A = 2m - 1 . s - 1 . Não há componente ou variação d
O campo de velocidade, para uma fonte plana localizada a uma distância h = 1m acima de uma parede infinita alinhada ao longo do eixo x , é dado por: V → = q 2 π x 2 + y - h 2 x i → + y - h j → + q 2 π
5.87 O perfil de velocidade para o escoamento inteiramente desenvolvido em um tubo circular é V r = V m á x 1 - r R 2 á . Avalie as taxas de deformação linear e angular para este escoamento. Obtenha u