Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 55
Em um funil cônico, com meio ângulo , o líquido é drenado através de um pequeno orifício de diâmetro no vértice do funil. A velocidade do líquido através do orifício é dada, aproximadamente, por , em que é a altura da superfície livre do líquido acima do orifício. Inicialmente, o funil está cheio até uma altura . Obtenha uma expressão para o tempo, , de drenagem do funil. Encontre o tempo de drenagem de para (uma variação de profundidade de ), e de para o esvaziamento total (também uma variação de profundidade de ). Você pode explicar a discrepância desse tempo? Trace o gráfico do tempo de drenagem em função de para esse diâmetro variando de até .
Passo 1
Podemos fazer um diagrama do funil cônico da seguinte maneira:
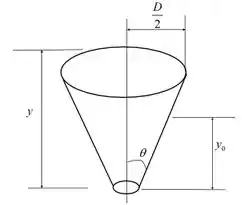
Podemos fazer as seguintes considerações:
Fluido incompressível.
Negligenciar a densidade do ar.
Fluxo uniforme.
Passo 2
Podemos começar a resolver a questão aplicando a equação de continuidade. Assim temos:
Pelas considerações feitas, e tratando o funil como o CV, a equação básica se torna seguinte maneira:
Passo 3
Pelo diagrama, podemos dizer que:
Aqui, é a altura do líquido é o ângulo do semi-cone. A área de do funil pode ser escrita da seguinte forma:
Substituindo , nós temos:
Temos também que a área do orifício é:
Passo 4
Assim, podemos substituir a área do funil e do orifício na equação da continuidade. Dessa forma teremos:
Substituindo por dito no enunciado, temos:
Passo 5
Podemos separa as variáveis e integras dos dois lados. Assim temos:
Portanto, a expressão para o tempo é:
Passo 6
Para encontrar o tempo para drenar, usamos a equação do tempo com a profundidade de . Assim, encontramos o tempo para drenagem.
Substituto,, , , e na equação tempo temos:
Passo 7
Para encontrar o tempo para drenar de para , usamos a equação do tempo com as duas profundidades. Assim, encontramos o tempo para drenar de e então a diferença é a tempo que queremos.
Substituto,, , , e na equação tempo temos:
Portanto o tempo para drenar de para é .
Passo 8
Para encontrar o tempo para drenar de para vazio, usamos a equação do tempo com a profundidade de .
Substituto,, , e na equação tempo temos:
De para é um pouco mais longa, porque, embora a taxa de fluxo diminua a área do funil também diminui.
Passo 9
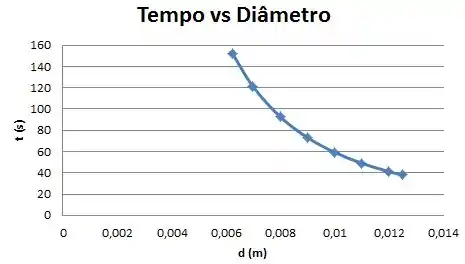
Para traçar o gráfico do tempo de drenagem em função de para esse diâmetro variando de até podemos substituir, , , na equação do tempo.
Usando a equação acima variando o diâmetro, podemos encontras os tempos de drenagem.
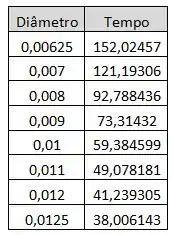
O gráfico de tempo pelo diâmetro foi plotado com uso do software Microsoft Excel com base na tabela acima.
