Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 80
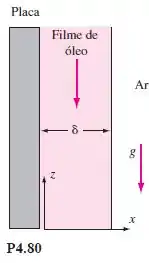
Óleo, de massa específica e viscosidade , é drenado continuamente por um lado de uma placa vertical, como na Figura P4.80. Após uma região de desenvolvimento próximo ao topo da placa, o filme de óleo se tornará independente de z e com espessura constante δ. Suponha que w = w(x) apenas e que a atmosfera não oferece resistência ao cisalhamento para a superfície do filme. (a) Resolva a equação de Navier-Stokes para w(x) e faça um esboço de sua forma aproximada. (b) Considere que a espessura do filme e a inclinação do perfil de velocidade na parede são medidos com um anemômetro doppler a laser (Capítulo 6). Encontre uma expressão para a viscosidade do óleo em função de .
Passo 1
Bora pra mais uma!
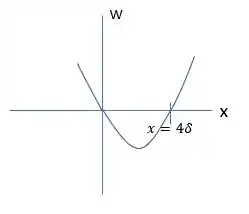
Primeiramente, não há um gradiente de pressão devido a pressão constante da atmosfera. O componente z da equação de Navier-Stokes é , e a solução da equação requer w=0 em x=0 e , ou seja, sem cisalhamento na borda do filme. Em , a solução se dá por:
É importante frisar que o sentido de w é apontado “para baixo”.
A inclinação do perfil de velocidade na parede é então obtida derivando a equação acima:
E obtemos a expressão para a viscosidade do óleo em função de simplesmente rearranjando a equação:
