Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 13

Para o escoamento do Problema 4.123, mostre que a variação da velocidade radial uniforme é Vr = Q/2πrh. Obtenha expressões para a componente r da aceleração de uma partícula fluida na fresta e para a variação de pressão como uma função da distância radial a partir dos orifícios centrais.

Passo 1

Pessoal, vamos aplicar a conservação de massa para um volume de controle no contorno de r:

0 = d d t ∫ ρ d V C V + ∫ ρ v → d A → S C

Assumindo regime permanente, fluido incompressível e fluxo uniforme pela seção, temos:

0 = ∫ v → d A → S C = ∑ Q s a i - Q e n t r a

Agora devemos ver pelo desenho o que isto significa. Temos 2 entradas de Q / 2 e uma saída que pode ser representada por (ver exercício 4.123):

Q s a i = V r   A = V r   2 π r h

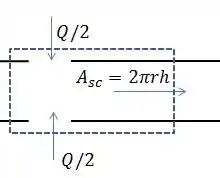
Então ficamos com a equação:

0 = V r   2 π r h - 2 Q 2

V r = Q 2 π r h

Passo 2

Para a variação de pressão, vamos usar a equação 6.3a do livro, que corresponde a coordenadas cilíndricas:

a r = ∂ V r ∂ t + V r ∂ V r ∂ r + V θ r ∂ V r ∂ θ + V z ∂ V r ∂ z - V θ 2 r = g r - 1 ρ ∂ p ∂ r

Sendo V z = 0 ;   V θ = 0 ;       V r = Q 2 π r h simplificamos a expressão:

a r = V r d V r d r

a r = Q 2 π r h d Q 2 π r h d r

a r = Q 2 π r h Q 2 π r h - 1 r 2

a r = - 1 r Q 2 π r h 2

a r = - V r 2 r

Passo 3

Ainda usando a equação anterior:

a r = g r - 1 ρ ∂ p ∂ r

Como g r = 0 , podemos encontrar a equação da variação de pressão:

- V r 2 r = - 1 ρ ∂ p ∂ r

∂ p ∂ r = ρ V r 2 r

Resposta

a r = - V r 2 r

∂ p ∂ r = ρ V r 2 r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.45 Considere o campo de velocidade no plano x y dado por V → = A x x 2 + y 2 i ^ + A y x 2 + y 2 j ^ , em que A = 10m 2 / s e x e y são medidos em metros. Este é um possível campo de escoamento inco
5.40 Considere o campo de escoamento dado por V → = a x 2 y i ^ - b y j ^ + c z 2 k ^ , em que a = 2m - 2 s - 1 , b = 2s - 1 e c = 1m - 1 s - 1 . Determine (a) o número de dimensões do escoamento, (b)
5.42 O campo de velocidade em uma camada-limite laminar é dado pela expressão V → = A U y x 1 2 i ^ + A U y 2 4 x 3 2 j ^ . Nesta expressão, A = 141m - 1 2 e U = 0,240m / s é a velocidade da corrente
5.57 Um campo de velocidade é representado pela expressão V → = A x - B i ^ - A y j ^ , em que A = 0,2s - 1 , B = 0,6ms - 1 e as coordenadas são medidas em metros. Obtenha uma expressão geral para a a
5.54 Um escoamento em onda de um fluido incompressível em uma superfície sólida segue um modelo senoidal. O escoamento é axissimétrico em torno do eixo z , o qual é normal à superfícies. A componente