Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 29

Escoamento de ar em regime permanente, incompressível e sem atrito, da direita para a esquerda sobre um cilindro circular estacionário de raio a, é dado pelo campo de velocidade:

V → = U a r 2 - 1 cos ⁡ θ   e ^ r + U a r 2 + 1 sin ⁡ θ   e ^ θ

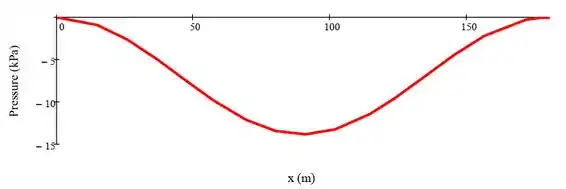
Considere o escoamento ao longo da linha de corrente que forma a superfície do cilindro, r = a. Obtenha uma expressão para a variação de pressão manométrica sobre a superfície do cilindro. Para U = 75 m/s e a = 150 mm, trace o gráfico da distribuição da pressão manométrica, e encontre a pressão mínima. Trace um gráfico da velocidade V como função de r ao longo da linha radial θ   = π / 2 para r > a (isto é, diretamente acima do cilindro), e explique.

Passo 1

Pessoal, para o campo de velocidade dado, devemos usar as equações de Euler com coordenadas cilíndricas:

ρ a r = ρ ∂ V r ∂ t + V r ∂ V r ∂ r + V θ r ∂ V r ∂ θ + V z ∂ V r ∂ z - V θ 2 r = ρ g r - ∂ p ∂ r

ρ a θ = ρ ∂ V θ ∂ t + V r ∂ V θ ∂ r + V θ r ∂ V θ ∂ θ + V z ∂ V θ ∂ z + V r V θ r = ρ g θ - 1 r ∂ p ∂ θ

Onde:

V r = U a r 2 - 1 cos ⁡ θ

V θ = U a r 2 + 1 sin ⁡ θ

V z = 0

Passo 2

Vamos ignorar a gravidade nesta questão. Para a equação em r, teremos:

ρ V r ∂ V r ∂ r + V θ r ∂ V r ∂ θ - V θ 2 r = - ∂ p ∂ r

Na superfície r = a , temos:

V r = 0

V θ = 2 U sin ⁡ θ

Substituindo os valores:

ρ - V θ 2 a = - ∂ p ∂ r

∂ p ∂ r = ρ V θ 2 a

∂ p ∂ r = ρ 2 U sin ⁡ θ 2 a

∂ p ∂ r = 4 ρ U sin 2 ⁡ θ   a

Passo 3

Vamos ignorar a gravidade nesta questão. Para a equação em θ , teremos:

ρ V r ∂ V θ ∂ r + V θ r ∂ V θ ∂ θ + V r V θ r = - 1 r ∂ p ∂ θ

Na superfície r = a , temos:

V r = 0

V θ = 2 U sin ⁡ θ

Substituindo os valores:

ρ V θ a ∂ V θ ∂ θ = - 1 r ∂ p ∂ θ

1 r ∂ p ∂ θ = - ρ 2 U sin ⁡ θ a ∂ ( 2 U sin ⁡ θ ) ∂ θ

1 r ∂ p ∂ θ = - ρ 2 U sin ⁡ θ a 2 U cos ⁡ θ

1 r ∂ p ∂ θ = - 4 U 2 ρ sin ⁡ θ cos ⁡ θ a

Então, o gradiente de pressão vale:

∇ p = 4 ρ U sin 2 ⁡ θ   a   e ^ r - 4 U 2 ρ sin ⁡ θ cos ⁡ θ a e ^ θ

∇ p = 4 ρ U a sin ⁡ θ ( sin ⁡ θ   e ^ r - cos ⁡ θ e ^ θ )

Passo 4

Vamos agora encontrar a distribuição de pressão, a partir da integral da expressão em θ :

d p = ∂ p ∂ θ d θ

∫ p a t m p d p = ∫ 0 θ ∂ p ∂ θ d θ

p - p a t m = ∫ 0 θ - 4 U 2 ρ sin ⁡ θ cos ⁡ θ d θ

p - p a t m = - 4 U 2 ρ - cos 2 ⁡ θ 2 θ 0

p - p a t m = 2 U 2 ρ cos 2 ⁡ θ - cos ⁡ 0

p - p a t m = 2 U 2 ρ cos 2 ⁡ θ - 1

p - p a t m = - 2 U 2 ρ sin 2 ⁡ θ

Como é pedida a pressão manométrica → p a t m = 0 :

p θ = - 2 U 2 ρ sin 2 ⁡ θ

A pressão mínima acontecera quando o seno for máximo θ = π 2 :

p π 2 = - 2 75 2 1,23 sin 2 ⁡ π 2

p π 2 = - 13,8   k P a

Resposta

∇ p = 4 ρ U a sin ⁡ θ ( sin ⁡ θ   e ^ r - cos ⁡ θ e ^ θ )

p θ = - 2 U 2 ρ sin 2 ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.84 Considere novamente o escoamento viscométrico do Exemplo 5.7. Avalie a taxa média de rotação de um par de segmentos de linhas perpendiculares, orientados a ± 45 ° em relação ao eixo x. Mostre que
5.66 Considere o escoamento incompressível de um fluido através de um bocal, conforme mostrado. A área do bocal é dada por A = A 0 1 - b x e a velocidade de entrada varia de acordo com U = U 0 0,5 + 0
5.67 Considere novamente o campo de velocidade bidimensional em regime permanente do Problema 5.56. Obtenha expressões para as coordenadas de partícula, x p = f 1 t e y p = f 2 t , como funções do tem
5.70 Expanda ( V → ⋅ ∇ ) V → em coordenadas cilíndricas pela substituição direta do vetor velocidade para obter a aceleração convectiva de uma partícula fluida. Compare os resultados com as Eqs. 5.12.
5.68 Considere o escoamento unidimensional e incompressível através do duto circular mostrado. A velocidade na seção 1 é dada por U = U 0 + U 1s e nω t , em que U 0 = 20m / s , U 1 = 2m / s e ω = 0,3r