Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 65

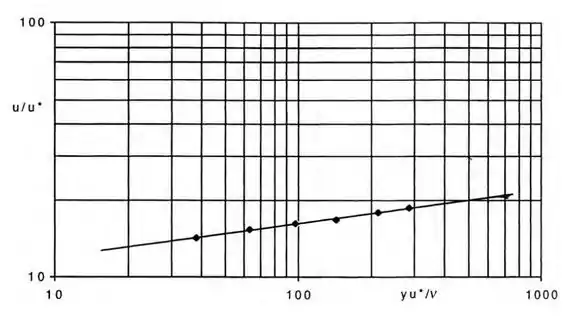
No escoamento turbulento próximo a uma parede plana, a velocidade local u varia apenas com a distância y da parede, com a tensão de cisalhamento na parede τ p e com as propriedades ρ e μ do fluido. Os dados a seguir foram obtidos no túnel de vento da Universidade de Rhode Island para escoamento de ar, ρ =   1,19 k g m 3 ,   μ =   1,82 E - 5 k g m . s e τ p =   1,39 Pa:

(a) Coloque esses dados em um gráfico na forma do adimensional u em função do adimensional y e proponha um ajuste de curva tipo lei de potência adequado. (b) Considere que a velocidade no túnel é aumentada para u = 27,43 m/s em y = 2,8 mm. Calcule a nova tensão de cisalhamento na parede em Pa.

Passo 1

Bora pra mais uma!

Sendo u = f c n y , τ w , ρ ,   μ ,   então n = 5 e j = 3 M L T . Então, esperamos n - j = 2   grupos pi. Que são escolhidos conforme abaixo:

u u * = f c n ρ u * y μ ,   s e n d o   u * = τ w ρ 1 2 = 1,39 P a 1,9 k g m 3 1 2 = 0,86 m / s .

Podemos então, modificar os parâmetros:

Plotemos então da forma logaritmo – logaritmo, note que os resultados são praticamente lineares:

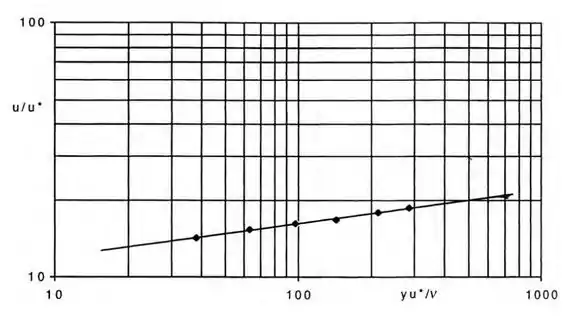
  1. Daqui, obtemos a inclinação da reta como sendo 0,13, e intercepta em ( y u * v = 1 ) em 8,9, daí:

    2. u u * ≈ 8,9 y u * v 1 3

  2. Agora, considerando a velocidade no túnel é aumentada para u = 27,43 m/s em y = 2,8 mm, podemos substituir em:

27,43 m s u * = 8,9 * 0,0028 m * u * 1,8 E - 5 k g m s 1 3 → u * = 1,5 m s

Daí:

τ w = ρ u * 2 = 1,5 m s 2 * 1,19 k g m 3 = 2,68 P a

Resposta

  1. u u * ≈ 8,9 y u * v 1 3

  2. τ w = 2,68 P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tensão de cisalhamento na parede τ p para escoamento em um espaço anular estreito entre um cilindro fixo e outro rotativo é uma função da massa específica ρ , da viscosidade μ , da velocidade angula
Uma viga simplesmente apoiada de diâmetro D, comprimento L e módulo de elasticidade E é submetida a um escoamento transversal de fluido de velocidade V, massa específica ρ e viscosidade μ . A deflexão
Um vertedouro é uma obstrução em um escoamento em canal que pode ser calibrado para medir a vazão, como mostra a figura abaixo. A vazão volumétrica Q varia com a gravidade g, com a largura b do verted
A taxa de perda de calor Q ˙ p e r d a através de uma janela ou parede é uma função da diferença de temperatura Δ T entre o ambiente interno e externo, da área A da superfície da janela e do valor de
O torque M requerido para acionar o viscosímetro do tipo cone-placa (mostrado abaixo) depende do raio R, da velocidade de rotação Ω , da viscosidade do fluido μ e do ângulo θ do cone. Reescreva essa r