Um rotor Savonius (Figura 6.29b) pode ser aproximado por dois semitubos abertos, como na Figura P7.96, montados em um eixo central. Se o arrasto de cada tubo é semelhante àquele da Tabela 7.2, deduza uma fórmula aproximada para a taxa de rotação Ω em função de

U, D, L e das propriedades do fluido (r, m).

Nosso primeiro passo será encontrar uma expressão para o torque .

Pra isso, vamos considerar o esquema abaixo:

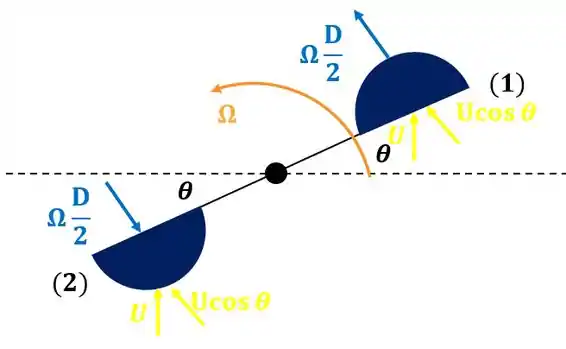
Como vocês podem ver, temos um ângulo de varredura entre a barra e o eixo horizontal. Dessa maneira, temos a componente da velocidade da velocidade agindo nos dois semitubos.

Além disso, também temos a velocidade devido à rotação da barra agindo dois semitubos que leva em conta a velocidade angular e o diâmetro dos semitubos, ou seja .

Sendo assim, podemos fazer um balanço de momento, considerando a linha de ação da força de arrasto dos dois semitubos:

Agora, vamos achar os coeficientes de arrasto e .

Eles podem ser encontrados na Tabela 7.2, Página 493 , como na imagem:

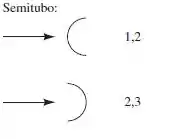
Ou seja, e .

Além disso, devemos calcular as velocidades relativas e . Pra isso, devemos fazer um balanço entre as velocidades e , levando em consideração os sentidos delas.

Na primeira delas, as velocidades estão no mesmo sentido, e, portanto, . Na segunda, as velocidades têm sentido diferente, e, portanto,.

Substituindo no nosso balanço:

Além disso, o torque é zero, e, portanto ficamos com:

Vamo finalizar a questão agora.

Primeiro, vamos tirar a raiz quadrada de ambos os lados:

Podemos então reagrupar os termos e isolar :

Como achamos e no passo anterior, sabemos que

E agora, devemos entender que a média de

Além disso, pra fazer uma simplificação, devemos considerar que o torque médio de se repete cada ângulo de . Dessa maneira, definimos que a média de variando de a , é .

Substituindo tudo isso na equação acima, vamos ter:

E agora, isolando e resolvendo pra :

Pronto, matamos a questão juntos!