Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 168
Um foguete de “construção caseira”, a combustível sólido, tem uma massa inicial de ; são de combustível. O foguete é lançado verticalmente para cima a partir do repouso, queimo combustível a uma taxa constante de e expele os gases de combustão a uma velocidade de em relação ao foguete. Considere que a pressão na saída seja atmosférica e que a resistência do ar possa ser desprezada. Calcule a velocidade do foguete e a distância percorrida por ele após o lançamento. Trace o gráfico da velocidade do foguete e a distância percorrida como funções do tempo.
Passo 1
Considerações Iniciais:
- Escoamento em estado estacionário;
- Escoamento incompressível;
- Escoamento com velocidade constante;
- Escoamento uniforme.
- Força de resistência desprezível.
Passo 2
Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:
Como estamos analisando um sistema , temos:
Não há resistência, então, :
Não temos a variação das propriedades com o tempo, então:
Assim:
Então:
Passo 3
Como e :
Assim:
Integrando:
Passo 4
Calculando a velocidade do foguete após o lançamento.
Sendo:
;
;
;
.
Então:
Passo 5
Como , temos:
Integrando com auxílio de programas matemáticos:
Passo 6
Calculando a distância percorrida pelo foguete após o lançamento.
Passo 7
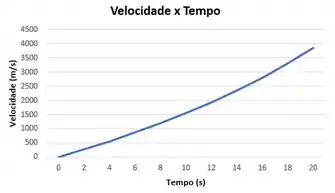
Traçando o gráfico da velocidade do foguete e da distância percorrida como funções do tempo.
