Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 77

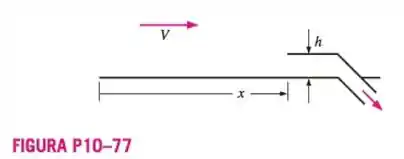
Para evitar a interferência da camada limite, os engenheiros desenham uma “cavidade de camada limite” para afinar a camada limite em um túnel de vento grande (Figura P10-77). A cavidade é construída com chapa fina de metal. O ar está a 20 °C e flui à velocidade V = 65,0 m/s. A que altura (dimensão h) deverá estar a cavidade na distância a jusante x = 1,45 m?

Passo 1

Para descobrir a que altura deverá estar a cavidade na distância a jusante, precisamos descobrir qual será a espessura da camada limite nesse ponto.

Para começar vamos dar um pulo lá na tabela A.9 do apêndice A para pegar as propriedades de interesse do ar a temperatura de 20 °C, então teremos:

Agora, com isso, e sabendo que o número de Reynolds é dado por:

Substituindo os valores conhecidos para a seção a jusante, teremos:

Então, como o número de Reynolds crítico para camada limite turbulenta é dado por:

Temos o nosso número de Reynolds a jusante maior que o número para escoamento turbulento, então vamos adotar escoamento turbulento ao longo da distância .

Passo 2

Agora, para resolver o problema e encontrar o valor da espessura da camada limite, vamos recorrer à tabela 10-4 vista nessa seção, onde teremos duas equações para calcular a espessura. Vamos utilizar primeiro aquela obtida a partir da lei da potência de um sétimo, que é dada por:

Substituindo os valores conhecidos, teremos:

Passo 3

Agora, através da equação obtida pela lei da potência de um sétimo combinada com dados empíricos para escoamento turbulento através de dutos lisos, teremos:

Substituindo os valores conhecidos, chegamos em:

Então podemos ver que a altura deverá ser aproximadamente 0,025 m.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A componente de velocidade na direção da corrente da camada limite sobre placa plana permanente, incompressível, laminar e com espessura δ é aproximada pelo perfil de onda senoidal do Problema 10 - 85

A componente da velocidade na corrente de uma camada limite sobre placa plana permanente, incompressível, laminar e de espessura d é aproximada pela expressão linear simples, u = U y / δ para yδ e u =

Normalmente pensamos nas camadas limite como se elas estivessem ocorrendo ao longo de paredes sólidas. No entanto, há outras situações de escoamento nas quais a aproximaçãoda camada limite também é ap

Neste capítulo, afirmamos que a aproximação de camada limite estabelece uma “ponte” entre a equação de Euler e a equação de Navier-Stokes. Explique.

Considere uma região irrotacional de escoamento planar no plano r θ . Mostre que a função de corrente ψ satisfaz a equação de Laplace em coordenadas cilíndricas.