Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 129

Um experimento de atrito em tubo, usando água, deve ser projetado para atingir número de Reynolds de 100.000. O sistema usará tubo liso de PVC de 5 cm de um tanque de nível constante até a bancada de teste e 20 m de tubo liso de PVC de 2,5 cm montados horizontalmente para a seção de teste. O nível de água no tanque de altura de carga constante é 0,5 m acima da entrada para o tubo de PVC de 5 cm. Determine a velocidade média da água requerida no tubo de 2,5 cm. Verifique a viabilidade do uso de um tanque de altura de carga constante. Calcule a diferença de pressão esperada entre tomadas distanciadas de 5 m na seção horizontal de teste.

Passo 1

Oi pessoal, tudo bem ?

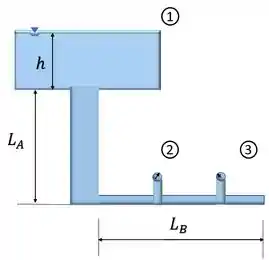
Eis um esboço do esquema descrito pelo enunciado.

Para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga:

P 1 ρ ∙ g +   α ∙ V 1 2 2 g + z 1 =   P 2 ρ ∙ g +   α ∙ V 2 2 2 g + z 2   +   h p

Considerações: α = 1

Podemos ignorar as pequenas perdas no tubo

h = 0,5 m

As perdas de carga serão representadas pela perda de carga em A e em B, resultando em:

h p = f A V A 2 L A 2 g D A + f B V B 2 L B 2 g D B

Passo 2

O problema quer R e B = 10 5

Sabe-se que

R e B = V B D B     υ         →       V B = R e B υ D B = 10 5 * 1,01 * 10 - 6 0,025                     →     V B = 4,04 m s

Obs: O valor da viscosidade dinâmica foi encontrado no Apêndice A, para água à 20ºC.

Para o cálculo de V A , temos:

V A = V B D B D A 2       →             V A = 4 * 2,5 5 2               →       V A = 1,01 m s

Então, o R e A recebe:

R e A = V A D A     υ         →       1,01 * 0,05 1,01 * 10 - 6                     →     R A = 5 * 10 4

Passo 3

Para tubo PVC, e = 0,0015 m m

Percebe-se que os dois tubos possuem escoamento turbulento, portanto:

1 f = - 2 ∙ l o g ⁡ ( e D 3,7 + 2,51 R e ∙ f )

Utilizando a ferramenta Solve do excel, foi possível determinar o fator de atrito:

f A = 0,021   e   f B = 0,0183

Passo 4

Agora, aplicando a equação da energia entre os pontos 1 e 3, representados no esquema:

g L A + h - V B 2 2 = f A V A 2 L A 2 D A + f B V B 2 L B 2 D B    

Ao isolar L A e substituir os valores na equação acima, temos que:

L A = 12,8 m

A maioria dos tetos tem cerca de 3,5 m ou 4 m, portanto, essa altura é IMPRÁTICA

Resposta

Aplicando a equação da energia entre os pontos 2 e 3, temos:

P 2 ρ + V B 2 2 - P 3 ρ + V B 2 2 = f B V B 2 L B 2 D B         →       Δ p = ρ f B L B V B 2 D B 2

Portanto, a variação de pressão Δ p é:

Δ p = 29,9 k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um experimento de bancada consiste em um reservatório com um tubo longo e horizontal de 500 mm de comprimento e diâmetro 7,5 mm ligado em sua base. O tubo sai de um tanque. O escoamento de água a 10°C
Uma piscina pequena é drenada usando uma mangueira de jardim. A mangueira tem 20 mm de diâmetro interno, uma rugosidade absoluta de 0,2 mm e 30 m de comprimento. A extremidade livre da mangueira está
Dados foram obtidos por medições em um trecho vertical de tubo de ferro galvanizado, velho e corroído, com diâmetro interno de 50 mm. Em uma seção a pressão era p1 = 750 kPa (manométrica); em uma segu
Em uma instalação de arcondicionado, é requerida uma vazão de 35 m3/min de ar a 10°C. Um duto de chapa de aço lisa de seção retangular (0,23 m por 0,75 m) é usado. Determine a queda de pressão (em mm
O escoamento em um tubo pode alternar entre os regimes laminar e turbulento para números de Reynolds na zona de transição. Projete uma bancada de testes consistindo de um cilindro transparente de plás