Um experimento de laboratório envolve transferência simultânea de calor e de massa em uma toalha embebida com água, submetida a irradiação proveniente de um conjunto de lâmpadas radiantes e a um escoamento paralelo de ar sobre a sua superfície. Usando uma correlação convectiva a ser apresentada no Capítulo 7, o coeficiente de transferência de calor por

convecção médio é estimado em . Considere que as propriedades radiantes da toalha são iguais às da água, . A vizinhança se encontra a 300 K.

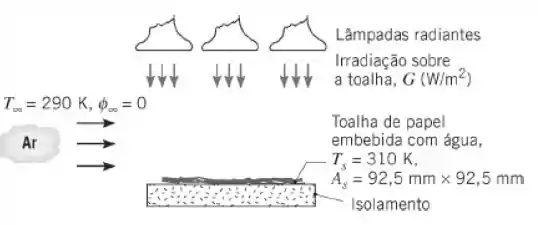
1. Determine a taxa na qual a água evapora da toalha, .
2. Efetue um balanço de energia na toalha para determinar a taxa líquida de transferência por radiação, , para a toalha. Determine a irradiação .

Para isso nós podemos usar a relação:

Onde é a densidade, o calor específico a pressão constante, o número de Lewis.

O número de Lewis também pode ser escrito como:

Onde é a difusividade térmica e a difusividade mássica!!

Para a maioria das aplicações

Sabendo que:

Na Tabela A.4 para nossa temperatura média de 300 K nós temos:

E na Tabela A.8 para o vapor de água e o ar:

Substituindo:

Colocando na fórmula do Passo 1:

Na letra (b) nós queremos achar a um balanço de energia na toalha para determinar a taxa líquida de transferência por radiação, , para a toalha.

Neste caso nós temos o calor por convecção sendo transferido para a toalha, assim como radiação, e liberando calor por meio da evaporação da água:

A transferência de calor por evaporação é dada por:

Já o calor por convecção é calculado como:

Nosso balanço ficará assim:

E aí? Acabamos?

Que nada !! Ainda precisamos determinar a irradiação !!

A irradiação se relaciona com a transferência de calor por radiação:

Lembrando que:

E assumindo que a temperatura da vizinhança será a temperatura média:

Substituindo na fórmula:

E chegamos ao fim de mais umaa !!